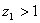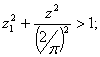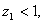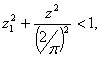Исследование движения смеси на наклонной плоскости

4.2 Исследование движения смеси на наклонной плоскости

Закономерности движения частицы, идеализируемой в виде материальной точки по вибрирующей шероховатой поверхности, представляют интерес не только для теории вибротранспортирования и вибросепарациии тел малых размеров, но также и для описания более сложных процессов, например, вибрационного разделения сыпучих смесей, вибротранспортирования и сепарации твердых или упругих тел конечных размеров, а также слоя сыпучего материала. Дифференциальные уравнения движения частиц по вибрирующей шероховатой поверхности играют в теории указанных процессов почти столь же фундаментальную роль, что и уравнение движения маятника в общей теории колебаний.

Приводимые ниже результаты относятся к случаю, когда вибрирующая поверхность является плоской и совершает поступательные колебания, а поле задаваемых сил, действующих на частицу, однородно и, в частности, представляет собой поле силы тяжести. Эти результаты, однако, могут быть использованы и в общем случае, если перемещение частицы по поверхности за период колебаний мало по сравнению с радиусом кривизны поверхности, а также с расстояниями, на которых траектории колебаний и задаваемые силы претерпевают сколько-нибудь существенные изменения.

Дифференциальные уравнения относительного движения частицы в осях xOy, жестко связанных с вибрирующей плоскостью, в рассматриваемом случае имеют вид (ось Ox направлена вдоль, а ось Oy - нормально плоскости)

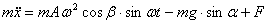
· (4.6)

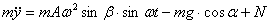
· (4.7)

где m - масса частицы; А и ω - соответственно амплитуда и частота колебаний;
β - угол наклона траектории колебаний относительно плоскости (угол вибрации);
α - угол наклона плоскости к горизонту;
g - ускорение свободного падения;
N - нормальная реакция;
F - сила сопротивления движению частицы, которую в начале будем считать силой сухого трения. При движении частицы по вибрирующей поверхности (у ≡ 0)

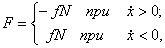
· (4.8)

где f - коэффициент трения скольжения, а нормальная реакция определяется из (4.7):

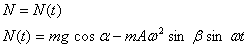
· (4.9)

При движении частицы без отрыва от поверхности ("без подбрасывания"), ,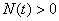

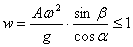
· (4.10)

Параметр w, равный отношению амплитуды поперечной составляющий переносной силы инерции 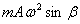к поперечной составляющей силы тяжести 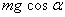, назовем параметром перегрузки. При относительном покое частицы на поверхности ( 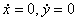,) сила сухого трения 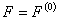не определяется (4.8), а находится из (4.6):

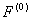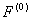
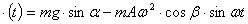
Состояние относительного покоя при этом сохраняется до тех пор, пока выполняется условие:

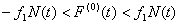
где ƒ₁ - коэффициент трения покоя, ƒ₁ ≥ ƒ.

Уравнение скольжения частицы по поверхности (y ≡ 0) получается из (4.6) при учете (4.8) и (4.9):

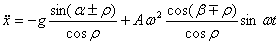
где 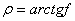- угол трения скольжения; верхние знаки соответствуют скольжению частицы вперед ( 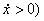, а нижние - назад ( 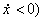. Уравнения полета частицы 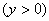получаются из (4.6) при 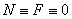. К выписанным соотношениям необходимо добавить равенства, определяющие закон изменения соотношения относительной скорости частицы при ее соударении с поверхностью. Обычно соударение считают мгновенным, а изменение нормальной составляющей скорости определяют в соответствии с гипотезой Ньютона:

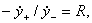
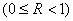
где 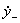и 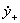- поперечные проекции скорости частицы до и после удара;
R - коэффициент восстановления.

В качестве связи продольных проекций скоросте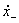й и 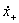до и после удара применительно к большему числу приложений целесообразно принять соотношения: а) "λ-гипотеза":

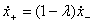· при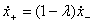

· (4.11)

Состояние относительного покоя при этом сохраняется до тех пор, пока выполняется условие:

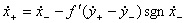· при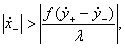

· (4.12)

где f'- коэффициент ударного трения, также часто принимаемый равным f.

Соотношения (4.11), (4.12) представляют собой достаточно грубые приближения, дающие, однако, при соответствующем выборе постоянных R, λ и f хорошее согласие экспериментальных и теоретических значений скорости вибротранспортирования.

При определенных условиях, кроме силы сухого трения, необходимо учитывать также и силу вязкого сопротивления движению частицы в окружающей ее среде. При этом также используют две гипотезы: в одном случае сила сопротивления считается пропорциональной первой или более высоким степеням относительной, а в другом - абсолютной скорости движения частицы. Для решения вопроса о необходимости учета силы вязкого сопротивления нужно оценить отношение этой силы

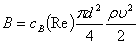· к силе сухого трения F=fmg

где d - размер частицы;
ν - ее скорость относительно среды, которую обычно можно считать имеющей порядок R?;
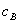- коэффициент сопротивления, зависимость которого от числа Рейнольдса 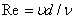(ν - коэффициент кинематической вязкости) определяется хорошо известным графиком, приводимым во многих руководствах по прикладной гидромеханике.

Так, для ν=0,15 см2/с и ρ=1,2• 10-3г/см3 (воздух при 20° С), f=0,5 в координатах ν=Aω, d сила B составляет не более 10% от fmg при плотностях частицы ρm, равных 0,4; 1,0 и 3,0 г/см3. Сопротивление воздуха необходимо учитывать при относительно мелких и относительно легких частицах. В общем случае частица может находиться относительно вибрирующей поверхности в одном из следующих четырех состояний: относительного покоя 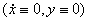, скольжения вперед 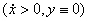, скольжения назад 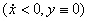, и отрыва 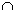, обозначим указанные состояния, соответственно, символами: 0,+,- и .

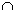Наибольший практический интерес представляют режимы движения частиц, характеризующиеся циклическим чередованием указанных состояний (этап движения), причем время одного цикла, называемое периодом переключений режима , равно или в целое число p раз превышает период колебаний поверхности . Такие режимы, как правило, устанавливаются по истечении некоторого времени после попадания частицы на поверхность или после возникновения колебаний поверхности.

Каждый установившийся режим может быть охарактеризован определенным набором циклически повторяющихся символов 0,+,- и , а также кратностью р и моментами перехода от одного этапа движения к другому. При этом достаточно указать лишь чередование символов и значения моментов в пределах одного периода переключений.

Запись вида

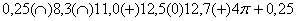
назовем формулой установившегося режима; эта запись указывает, что начиная с момента соответствующего значения фазового угла от 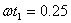до 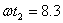, частица находится в полете над поверхностью, при 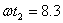происходит мгновенное соударение с поверхностью, снова полет до момента 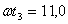, скольжение вперед по поверхности до момента 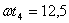, затем имеет место относительный покой до 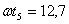и, наконец, скольжения вперед до 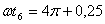. После этого цикл повторяется. Период переключения данного режима

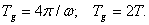
Для относительно небольших углов наклона α плоской поверхности к горизонту характерны установившиеся режимы, при которых частица за каждый период переключений перемещаются вдоль поверхности на равные расстояния, так что средняя скорость движения V, называемая в этом случае скоростью вибротранспортирования или виброперемещения, остается неизменной, и решения уравнения (4.6) имеют вид:

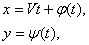· при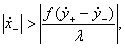

· (4.13)

где V - постоянная, а φ(t) и ψ(t) - периодические функции t с периодом, равным периоду переключений Tп; такие режимы назовем регулярными. Установившиеся режимы характерны, преимущественно, для значительных углов наклона плоской поверхности к горизонту. В этих режимах неизменное значение сохраняет среднее за период ускорение частицы W_m. Решения уравнений (4.6), соответствующие этим режимам, имеют вид:

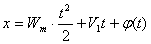
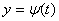
Выяснение характера, а также областей существования различных устойчивых установившихся режимов движения частицы является одной из основных задач теории. При этом целесообразно ограничиться исследованием устойчивости движения не относительно координат частицы и ее скоростей, а относительно упомянутых выше моментов перехода . Соответствующее определение устойчивости вполне аналогично определению устойчивости по Ляпунову, хотя и является "менее жестким", так как возможны режимы неустойчивости по Ляпунову, но устойчивые по моментам перехода. С математической точки зрения, рассматриваемая задача сводится к изучению решений нелинейных дифференциальных уравнений, которые в каждой из определенных частей фазового пространства являются линейными, однако имеют в каждой такой части различную аналитическую запись и даже различный порядок. Аналитическое решение подобной задачи может быть выполнено точными методами - так называемым обратным методом, а также методами поэтапного интегрирования, припасовывания, точечных отображений. Могут быть использованы и приближенные методы - гармонического баланса и прямого разделения движений. Помимо аналитических методов можно использовать графические построения, а также вычислительные машины.

Ниже, без воспроизведения процесса решения задачи, приведены лишь окончательные результаты.

Установившиеся режимы при отсутствии подбрасывания. Движение частицы без отрыва от вибрирующей поверхности может иметь место лишь при выполнении условия, что параметр перегрузки .
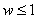Условия существования и устойчивости всех возможных установившихся режимов движения частицы при отсутствии подбрасывания могут быть выражены через четыре безразмерных параметра:

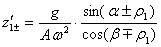
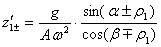
· (4.14)

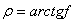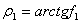( и - соответственно, углы трения покоя и скольжения), наряду с которыми введем также параметры:

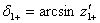
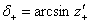
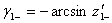
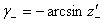
И функции этих параметров:

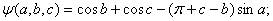
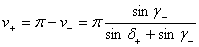
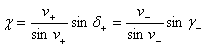
функция f(a,b) будет являться решением трансцендентного уравнения

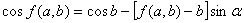
При |a|>p возможны ускоренные движения частицы. Все регулярные режимы имеют период переключений, совпадающий с периодом колебаний поверхности T и, если исключить тривиальный случай абсолютного покоя, могут быть всего четырех видов (с двумя подвидами А и Б, отвечающими режимам 3 и 4). В режимах 1,3, и 4 имеются движения частицы вперед и назад с мгновенными остановками. В режимах 4А и 4Б частица скользит только в одном направлении, в то время как при прочих режимах имеются этапы скольжения, как в положительном, так и в отрицательном направлениях.

Условия существования каждого режима распадаются на две группы соотношений, которые переходят одна в другую. В некоторых случаях допустимо считать коэффициенты трения покоя и скольжения f1 и f одинаковыми. При этом согласно (4.14):

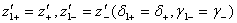
т.е. число определяющих безразмерных параметров становится равным двум, и области существования установившихся режимов могут быть изображены на плоскости.

Квадранту плоскости, определяемому неравенствами 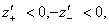соответствуют реально невозможные значения параметров, поскольку, согласно (4.14), указанные неравенства сводятся к требованию одновременного выполнения противоречивых соотношени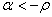й и ( ).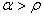

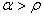В рассматриваемом случае f1=f вся область возможных значени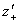й и 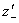заполнена областями существования рассмотренных режимов, и области существования отдельных режимов не налагаются друг на друга. Поэтому каждой комбинации значений параметров системы в данном случае отвечает некоторый, вполне определенный режим движения.

Аналогичное положение имеет место, когда коэффициенты трения f1 и f неодинаковы, но угол наклона плоской поверхности к горизонту меньше по модулю угла трения скольжения 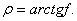При этом ускоренное движение частицы не может иметь места. Условия существования каждого из регулярных режимов и относительного покоя во всех случаях таковы, что при выполнении условий существования какого-либо одного из этих режимов не выполняются условия существования прочих. Когда угол наклона лотка к горизонту больше угла трения скольжения, но меньше угла трения покоя, 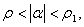т.е. то даже при отсутствии вибрации поверхности в зависимости от начальных условий частица с постоянным ускорением, скользит вниз.

При вибрации, в случае выполнения 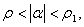также могут одновременно существовать два режима движения, один из которых - регулярный режим (в частности, относительный покой), а другой является безостановочным ускоренным движением вниз. Если из двух возможных режимов движения один устойчив, а другой неустойчив, в действительности реализуется устойчивый режим. Если оба режима устойчивы, то характер возникающего установившегося режима зависят от начальных условий. При достаточно большой амплитуде ускорения Аω² всегда имеет место ускоренное движение частицы вниз.

Аналогичное положение наблюдается и в случае 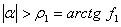, когда невозможны режимы с остановками и существует лишь один установившейся режим движения частицы - безостановочное ускоренное скольжение вниз по поверхности. В этом случае безостановочное движение устойчиво по моментам перехода в "большом" (хотя и не устойчиво по Ляпунову), так как в это движение переходит с течением времени любое другое движение, в котором скольжение частицы вниз началось в произвольный момент времени 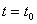. В случае, когда 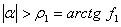, т.е. когда угол наклона плоской поверхности к горизонту по абсолютной величине большой угла трения, также имеет место "однозначность", а именно в этом случае, независимо от значений других параметров, всегда имеет место ускоренное движение частицы вниз по поверхности. При 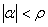все возможные установившиеся режимы движения определяются неравенствами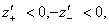

Итак, все возможные установившиеся режимы движения частицы при отсутствии подбрасывания устойчивы (по крайней мере, в "малом") во всей области их существования, за исключением, быть может, их границы. Более сложная картина характерна для случая движения с подбрасыванием, когда области устойчивости установившихся режимов движения не совпадают с областями их существования. Наибольший интерес для приложений представляет определение средней скорости и ускорения частицы в установившихся режимах движения. Их вычисление не вызывает существенных затруднений, если найдены моменты перехода от одного этапа к другому в установившемся движении; после этого дело сводится к легко выполняемому интегрированию (4.6).

В результате находится перемещение частицы S за один период переключений 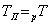для регулярных режимов и приращение скорости за тот же период 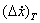для режимов ускоренных, а затем средние скорость и ускорение:

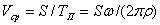
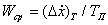
Для практических расчетов удобно пользоваться программой PAVN. В программе автоматически проверяется области применения гипотез взаимодействия частиц с лотком. Режимы без подбрасывания. В случае, когда допустимо считать, что f1=f, определение Vср значительно облегчается

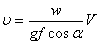
В случае чисто продольных колебаний плоской поверхности (β=0) подбрасывание частицы отсутствует при любых значениях параметров.

Однако в наиболее важном режиме 2 (типа + -) средняя скорость движения частицы составит

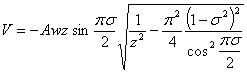
· (4.15)

где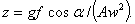

Указанный режим имеет место при 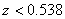, т.е. при достаточно интенсивных колебаниях поверхности.

В еще более частном, но имеющем важные приложения случае чисто продольных колебаний горизонтальной поверхности 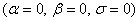средняя скорость частицы V в установившихся режимах согласно (4.15) равно нулю. В этом случае возможны три вида установившихся состояний частицы:

относительный покой (..);
колебания вблизи некоторого среднего положения с остановками конечной продолжительности после скольжения вперед и назад (режим 1 типа +…-…);
колебания вблизи среднего положения с мгновенными остановками после каждого скольжения (режим 2 типа = -). Области существования этих режимов в общем случае, когда ƒ₁≥ƒ, определяются соответственно неравенствами

Проведенные исследования показывают, что с увеличением угла наклона скорость транспортирования возрастает, при этом для тихоходных режимов наблюдается более интенсивное увеличение скорости. Благоприятно сказывается также уменьшение угла вибрации. Однако увеличение угла наклона не обеспечивает резкого повышения скорости. При транспортировании на подъем скорость весьма существенно снижается

Таким образом, хотя вибротранспортирование под уклон и повышает скорость перемещения, но, как правило, существенно не превосходит амплитудных значений скорости колебаний несущего органа. При перемещении под уклон для повышения скоростей транспортирования следует увеличить амплитуду колебаний, снижать угол вибрации и частоту колебаний.