
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Примерные примеры для итоговой аттестации по дисциплинам:
Примерные примеры для итоговой аттестации по дисциплинам:
Элементы высшей математики
Дискретная математика с элементами математической логики
Теория вероятностей и математическая статистика
1.Найдите комплексные корни уравнения 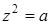 , если:
, если:
а) 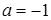 ; б)
; б) 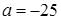 ; в)
; в) 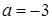 .
.
2.С помощью равносильных преобразований упростите высказывание
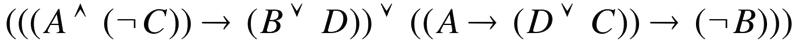
3.Группа учащихся изучает 7 учебных дисциплин. Сколькими способами можно составить расписание занятий на понедельник, если в этот день недели должно быть 4 различных урока?
1.Найдите x и y,для которых  .
.
2.Упростить формулу (А Ú В) Ù (А Ú С).
3.Сколько шестизначных чисел, кратных пяти, можно составить из цифр 1, 2, 3, 4, 5, при условии, что в числе цифры не повторяются?
1.При каких действительных значениях x и y комплексные числа
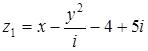 и
и 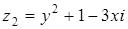
будут противоположными?
2.Привести к ДНФ: (PÚ Q )®R.
3.Подбрасывание игральной кости один раз.Событие А состоит в том,что выпавшеечисло очков – чётно.
1.Найтиlim (x4– 3x2+ 16x + 1)при х®–1.
2.Привести к КНФ: (PÙ(Q®R))®S.
3.Подбрасывание симметричной монеты 2 раза. Событие А состоит в том, что выпало ровно 2 герба.
1.Найти 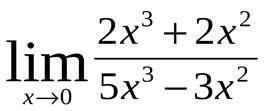 .
.
2.Привести к ДНФ формулу: 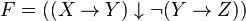
3.Вытягивание шара из урны,содержащей2белых и3чёрных шара.Событие А состоит в том, что вытянули чёрный шар.
1.Найти 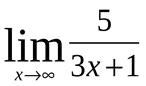 .
.
2.Привести к ДНФ: (PÚ Q )®R.
3.Набирая номер телефона,абонент забыл две последние цифры.Какова вероятностьтого, что он с первого раза наберёт эти цифры правильно, если он помнит, что они различны?
1.Найти 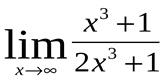 .
.
2.Привести к КНФ: (PÙ(Q®R))®S.
3.Шесть шариков случайным образом располагаются в шести ящиках так,что длякаждого шарика равновероятно попадание в любой ящик и в одном ящике может находиться несколько шариков. Какова вероятность того, что в каждом ящике окажется по одному шарику?
1.Найти 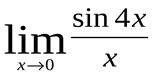 .
.
2.Привести к КНФ формулу 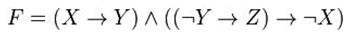
3.В урне 3 белых и 4 чёрных шара. Из урны вынимаются два шара. Найти вероятность того, что оба шара будут белыми.
1.Найти 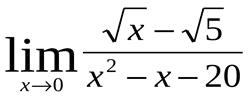 .
.
2.Пусть булева функция задана таблицей истинности.
а) составить СДНФ для данной функции; б) минимизировать СДНФ; в) построить логическую схему, реализующую данную функцию.
| x | y | z | F(x,y,z) | |||||||||||||
|
|
| |||||||||||||||
3.Завод производит85 %продукции первого сорта и10 % –второго.Остальныеизделия считаются браком. Какова вероятность, что взяв наудачу изделие, мы получим брак?
1.Построить график функции у = х × ех
2.Дана функция F(x,y,z) = 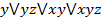 построить минимальную нормальную форму данной функции.
построить минимальную нормальную форму данной функции.
3.Из 20 студентов 5 человек сдали на двойку экзамен по истории, 4 – по английскому
языку, причём 3 студента получили двойки по обоим предметам. Каков процент студентов в группе, не имеющих двоек по этим предметам?
1.Вычислитеò(x3-3x +sin x)dx .
2.Построить минимальную форму для булевой функции, заданной таблично.
| x | y | z | F |
3.В урне лежит N шаров,из них n белых.Из неё достают шар и,не кладя егообратно, достают ещё один. Чему равна вероятность того, что оба шара белые?
1.Вычислитеò3+2x- x2dx .
2.Задайте множество А={x | х – целое неотрицательное и х+2=5} другим способом.
3.Из 30 экзаменационных билетов студент подготовил только 25. Если он отказывается отвечать по первому взятому билету (которого он не знает), то ему разрешается взять второй. Определить вероятность того, что второй билет окажется счастливым.
1.Вычислитеò(3x-4)3dx .
2. Выясните, равны ли множества: А={1, 2, 3}; В={2, 3, 1}.
3.По условиям предыдущего примера найти вероятность успешной сдачи экзамена, если для этого студент должен ответить на первый билет, или, не ответив на первый, обязательно ответить на второй.
1.Найти частные производные z = y4 –2xy2+ x2 + 2y + y2
2.Выясните, равны ли множества: А – множество всех равносторонних треугольников; В – множество всех равноугольных треугольников.
3.Литьё в болванках поступает из двух цехов:70 %из первого и30 %из второго.При этом продукция первого цеха имеет 10 % брака, а второго 20 %. Найти вероятность того, что одна взятая наугад болванка имеет дефект.
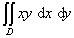
1.Вычислить двойной интеграл
2.Выясните, равны ли множества: А={1, 5, 8}; В={2, 8}.
3.В урне лежит N шаров, из которых n белых. Достаём из неё (без возвращения) два шара. Какова вероятность, что второй шар белый?
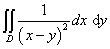
1.Вычислить двойной интеграл
2.Выясните, равны ли множества: А={0, 1}; В={{0, 1}}.
3.В продукции предприятия брак составляет 5 % от общего объема выпускаемых изделий. Для контроля качества случайно отобрано 20 изделий. Найти вероятность того, что среди них будет хотя бы одно бракованное.

1.Вычислить двойной интеграл
2.Даны множества А={1, 2}; В={a, b}. Найдите А´В, В´А.
3.Найти вероятность того, что при 10 бросках монеты орёл выпадет 3 раза.
1.Исследовать ряд на сходимость 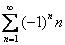 .
.
2.Изобразить на плоскости декартово произведение множеств А и В.
3.Абитуриент сдаёт два вступительных экзамена:по математике и физике.Составитьзакон распределения случайной величины х, числа полученных пятёрок, если вероятность получения пятёрки по математике равна 0,8, а по физике – 0,6.
1.Исследовать ряд на сходимость 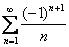 .
.
2.Даны числовые множества: А=[0,1], В=[0,1], С=[0,1]. Изобразите декартово произведение А´В´С.
3.Фермер считает,что,принимая во внимание различные потери и колебания цен,онсможет выручить не более 60 центов за десяток яиц и потерять не более 20 центов за десяток и что
| вероятности возможных выигрышей и потерь таковы: | ||||||
| Цена за 10 яиц | 0,6 | 0,4 | 0,2 | -0,2 | ||
| Р | 0,2 | 0,5 | 0,2 | 0,06 | 0,04 | |
Как оценить ожидаемую прибыль от продажи десятка яиц; от ожидаемых им в этом году 100000 яиц?
1.Исследовать ряд на сходимость 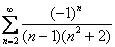 .
.
2.Даны два предиката А(х): х-2>0, B(x): x+2 ³ 0, зависящие от переменной х, хÎR. В чем заключаются предикаты А(х)ÈВ(х) и А(х)®В(х)?
3.Закон распределения случайной величины 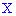 заданы функцией
заданы функцией
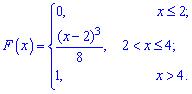
Найти плотность распределения вероятностей  и построить графики обеих функций
и построить графики обеих функций
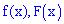 . Вычислить вероятность того, что случайная величина принадлежит промежутку
. Вычислить вероятность того, что случайная величина принадлежит промежутку
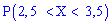 .
.
1.Решить дифференциальное уравнение 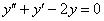 .
.
2.Дана формула ("x)(P(x) ® ($y)Q(x, y)) . Является ли она замкнутой?
3.Случайная величина 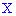 имеет закон распределения вероятностей в виде треугольника.
имеет закон распределения вероятностей в виде треугольника.
Записать выражения для плотности вероятностей и функции распределения вероятностей,
построить график 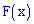 и вычислить
и вычислить  .
.
1.Решить дифференциальное уравнение 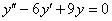 .
.
2.Дана формула ($x1 )("x2 )A1 (x1, x2 ) Ù A2 (x1, x2 ) Является ли она замкнутой?
3.Проведены испытания образцов дюралюминиевого профиля на разрыв.
Полученные значения предела прочности образцов (МПа) приведены в таблице
Найти точечные и интервальные оценки параметров распределения предела прочности при доверительной вероятности 0,95.
1.Решить однородное дифференциальное уравнение второго порядка 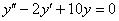
2.Множество R={(х,у):х – делитель у} определяет отношение на множестве А={1, 2, 3, 4, 5, 6}. Найдите все упорядоченные пары, ему принадлежащие. Изобразите граф, представляющий отношение R.
3.Группа учащихся изучает 7 учебных дисциплин. Сколькими способами можно составить расписание занятий на понедельник, если в этот день недели должно быть 4 различных урока?
1.Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям 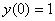 ,
,  .
.

2.Отношение R на множестве А = {а, b, с, d} задается матрицей:
| é0 | 0ù | ||
| ê | ú | ||
| ê0 | 1ú | ||
| ê0 | 0ú | ||
| ê | ú | ||
| ë1 | 0û |
порядок строк и столбцов в которой соответствует порядку выписанных элементов множества А.
Назовите упорядоченные пары, принадлежащие R.
3.Сколько шестизначных чисел, кратных пяти, можно составить из цифр 1, 2, 3, 4, 5, при условии, что в числе цифры не повторяются?
1.Чему равна матрица  , если матрица
, если матрица  ?
?
2.Даны множества А={1, 2, 3, 4}; В={3, 4, 6, 7}. Укажите отношения r1 и r2, одно из которых было бы функцией, а другое нет.
3.Сколько матчей будет сыграно в футбольном чемпионате с участием16команд,если каждые две команды встречаются между собой один раз?
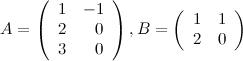
1.Задание. Вычислить  и
и 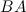 , если .
, если .
2.Какие из данных отношений являются отображениями?

А В А В А В
Рис. 1 Рис. 2 Рис. 3
3.Подбрасывание игральной кости один раз.Событие А состоит в том,что выпавшеечисло очков – чётно.
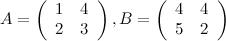
1.Найти 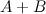 , если
, если
2.Пусть А=R=(-¥;+¥), xÎA. B=[0; +¥), yÎB. Зададим отношение ¦={(x,y)| y=x2}, ¦Ì А´В. Является ли данное отношение сюръекцией?
3.Подбрасывание симметричной монеты 2 раза. Событие А состоит в том, что выпало ровно 2 герба.
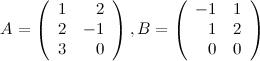
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|