Свойства сходящихся последовательностей

Последовательность 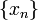элементов множества 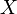называется неубывающей, если каждый элемент этой последовательности не превосходит следующего за ним.

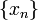— неубывающая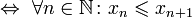

Последовательность 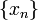элементов множества 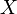называется убывающей, если каждый элемент этой последовательности превышает следующий за ним.

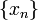— убывающая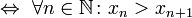

Последовательность называется монотонной, если она является неубывающей, либо невозрастающей.^[1]

Последовательность называется строго монотонной, если она является возрастающей, либо убывающей.

Очевидно, что строго монотонная последовательность является монотонной.

Иногда используется вариант терминологии, в котором термин «возрастающая последовательность» рассматривается в качестве синонима термина «неубывающая последовательность», а термин «убывающая последовательность» — в качестве синонима термина «невозрастающая последовательность». В таком случае возрастающие и убывающие последовательности из вышеприведённого определения называются «строго возрастающими» и «строго убывающими», соответственно.

Свойства сходящихся последовательностей

§ Всякая бесконечно малая последовательность является сходящейся. Её предел равен нулю.

§ Удаление любого конечного числа элементов из бесконечной последовательности не влияет ни на сходимость, ни на предел этой последовательности.

§ Любая сходящаяся последовательность элементов хаусдорфова пространства имеет только один предел.

§ Любая сходящаяся последовательность ограничена. Однако не любая ограниченная последовательность сходится.

§ Последовательность сходится тогда и только тогда, когда она является ограниченной и при этом её верхний и нижний пределы совпадают.

§ Если последовательность (x_n) сходится, но не является бесконечно малой, то, начиная с некоторого номера, определена последовательность (1 / x_n), которая является ограниченной.

§ Сумма сходящихся последовательностей также является сходящейся последовательностью.

§ Разность сходящихся последовательностей также является сходящейся последовательностью.

§ Произведение сходящихся последовательностей также является сходящейся последовательностью.

§ Частное двух сходящихся последовательностей определено, начиная с некоторого элемента, если только вторая последовательность не является бесконечно малой. Если частное двух сходящихся последовательностей определено, то оно представляет собой сходящуюся последовательность.

§ Если сходящаяся последовательность ограничена снизу, то никакая из её нижних граней не превышает её предела.

§ Если сходящаяся последовательность ограничена сверху, то её предел не превышает ни одной из её верхних граней.

§ Если для любого номера члены одной сходящейся последовательности не превышают членов другой сходящейся последовательности, то и предел первой последовательности также не превышает предела второй.

§ Если все элементы некоторой последовательности, начиная с некоторого номера, лежат на отрезке между соответствующими элементами двух других сходящихся к одному и тому же пределу последовательностей, то и эта последовательность также сходится к такому же пределу.

§ Любую сходящуюся последовательность (x_n) можно представить в виде (x_n) = (a + α_n), где a — предел последовательности (x_n), а α_n — некоторая бесконечно малая последовательность.

§ Всякая сходящаяся последовательность является фундаментальной. При этом фундаментальная числовая последовательность всегда сходится (как и любая фундаментальная последовательность элементов полного пространства).

Экспонента или число е

Р-рим числ. посл-ть с общим членом xn=(1+1/n)^n (в степени n)(1) . Оказывается, что посл-ть (1) монотонно возр-ет, ограничена сверху и сл-но явл-ся сходящейся, предел этой пос-ти наз-ся экспонентой и обозначается символом е»2,7128… Число е

Принцип вложенных отрезков

Пусть на числовой прямой задана посл-ть отрезков [a1,b1],[a2,b2],…,[an,bn],…

Причем эти отрезки удовл-ют сл. усл.:

1) каждый посл-щий вложен в предыдущий, т.е. [an+1,bn+1]Ì[an,bn], "n=1,2,…;

2) Длины отрезков ®0 с ростом n, т.е. lim(n®¥)(bn-an)=0. Посл-ть с указанными св-вами наз-ют вложенными.

Теорема Любая посл-ть вложенных отрезков содержит единную т-ку с принадлежащую всем отрезкам посл-ти одновременно, с общая точка всех отрезков к которой они стягиваются.

Док-во {an}-посл-ть левых концов отрезков явл. монотонно не убывающей и ограниченной сверху числом b1.

{bn}-посл-ть правых концов монотонно не возрастающей, поэтому эти посл-ти явл. сходящимися, т.е. сущ-ют числа с1=lim(n®¥)an и с2=lim(n®¥)bn => c1=c2 => c - их общее значение. Действительно имеет предел lim(n®¥)(bn-an)= lim(n®¥)(bn)- lim(n®¥)(an) в силу условия 2) o= lim(n®¥)(bn-an)=с2-с1=> с1=с2=с

Ясно что т. с общая для всех отрезков, поскольку "n an£c£bn. Теперь докажем что она одна.

Допустим что $ другая с‘ к которой стягиваются все отрезки. Если взять любые не пересекающиеся отрезки с и с‘, то с одной стороны весь “хвост” посл-тей {an},{bn} должен нах-ся в окрестностях т-ки с‘‘(т.к. an и bn сходятся к с и с‘ одновременно). Противоречие док-ет т-му.