На интегральную формулу Лапласа

На интегральную формулу Лапласа

Пример 26. В страховой компании 10 000 клиентов. Страховой взнос – 2 000 руб. Вероятность страхового случая 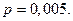Страховая выплата – 200 000 руб. Определить размер прибыли стразовой компании с вероятностью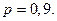

Пример 27. Страховая компания заключила 40000 договоров. Вероятность страхового случая по каждому из них в течение года составляет 2%. Найти вероятность, что таких случаев будет не более 870.

Теоремы сложения и умножения вероятностей. Независимость событий. Условная вероятность.

Пример 28. Три стрелка стреляют по одной мишени, и каждый попадает или промахивается независимо от результатов выстрелов других стрелков. Вероятности попадания в мишень для каждого из стрелков, соответственно, равны: 0,8; 0,7; 0,5. Определить вероятности следующих событий:

а) все три стрелка попали в мишень;

б) хотя бы один стрелок попал в мишень;

в) в мишень попали два стрелка.

Пример 29. Брошено три игральных кости. Найти вероятности следующих событий:

а) выпало три шестёрки;

б) выпало три шестёрки, если известно, что на одной из костей выпала шестёрка.

Пример 30. Из 20 студентов, находящихся в аудитории, 8 человек курят, 12 носят очки, а 6 и курят и носят очки. Одного из студентов вызвали к доске. Определим события А и В следующим образом: A = {вызванный студент курит}, B = {вызванный носит очки}.

Установить, зависимы события A и B или нет. Сделать предположение о характере влияния курения на зрение.

Пример 31. Студент знает 20 из 25 вопросов программы. Зачёт сдан, если студент ответит не менее чем на 3 из 4-х вопросов в билете. Взглянув на первый вопрос, студент обнаружил, что знает его. Какова вероятность, что студент сдаст зачёт?

Пример 32.Вероятность появления события в каждом из 400 независимых испытаний равна 0,8. Найти такое положительное число e, чтобы с вероятностью 0,99 абсолютная величина отклонения относительной частоты появления события от его вероятности не превышала e.

⇐ Предыдущая 1 234 Следующая ⇒