Лекционное занятие.. Системы двух линейных уравнений с двумя неизвестными.. Основные методы решения: подстановка, сложение или вычитание.. Определители второго порядка. Правило Крамера.. Исследование решений системы уравнений.. Метод подстановки.

Лекционное занятие.

Инструкция по выполнению:

1. Ознакомиться с теоретическим материалом.

2. Законспектируйте вкратце, выписав основные определения, формулы и т.д.

3. Фото проделанной работы отправить в личные сообщения https://vk.com/nemkova96 не позднее установленного срока.

Системы двух линейных уравнений с двумя неизвестными.

Основные методы решения: подстановка, сложение или вычитание.

Определители второго порядка. Правило Крамера.

Исследование решений системы уравнений.

Системы двух линейных уравнений с двумя неизвестными имеют вид:

где a, b, c, d, e, f – заданные числа; x, y – неизвестные. Числа a, b, d, e – коэффициенты при неизвестных; c, f – свободные члены. Решение этой системы уравнений может быть найдено двумя основными методами.

Метод подстановки.

1) Из одного уравнения выражаем одно из неизвестных, например x, через коэффициенты и другое неизвестноеy:

x = ( c – by ) / a . (2)

2) Подставляем во второе уравнение вместо x :

d ( c – by ) / a + ey = f .

3) Решая последнее уравнение, находим y :

y = ( af – cd ) / ( ae – bd ).

4) Подставляем это значение вместо y в выражение (2) :

x = ( ce – bf ) / ( ae – bd ) .

П р и м е р . Решить систему уравнений:

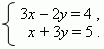
Из первого уравнения выразим х через коэффициенты и y :

x = ( 2y + 4 ) / 3 .

Подставляем это выражение во второе уравнение и находим y :

( 2y + 4 ) / 3 + 3y = 5 , откуда y = 1 .

Теперь находим х, подставляя найденное значение вместо y в

выражение для х: x = ( 2 · 1 + 4 ) / 3, откуда x = 2 .

Сложение или вычитание.Этот метод состоит в следующем.

1) Умножаем обе части 1-го уравнения системы (1) на (– d ), а обе части 2-го уравнения на а и складываем их:

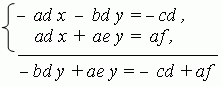
Отсюда получаем: y = ( af – cd ) / ( ae – bd ).

2) Подставляем найденное для y значение в любое уравнение системы (1):

ax + b( af – cd ) / ( ae – bd ) = c.

3) Находим другое неизвестное: x = ( ce – bf ) / ( ae – bd ).

П р и м е р . Решить систему уравнений:

методом сложения или вычитания.

Умножаем первое уравнение на –1, второе – на 3 и складываем их:

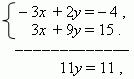
отсюда y = 1. Подставляем это значение во второе уравнение

(а в первое можно?): 3x + 9 = 15, отсюда x = 2.

Определители второго порядка.Мы видели, что формулы для решения системы двух линейных уравнений с двумя неизвестными имеют вид:

x = ( ce – bf ) / ( ae – bd ) ,

(3)

y = ( af – cd ) / ( ae – bd ) .

Эти формулы легко запоминаются, если ввести для их числителей и знаменателей следующий символ:

, который будет обозначать выражение: ps – qr .

Это выражение получается перекрёстным умножением чисел p, q, r, s :

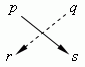
и последующим вычитанием одного произведения из другого: ps – qr. Знак « + » берётся для произведения чисел, лежащих на диагонали, идущей из левого верхнего числа к правому нижнему; знак « – » - для другой диагонали, идущей из правого верхнего числа к левому нижнему. Например,

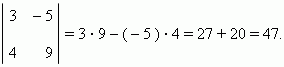
Выражение 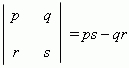называется определителем второго порядка.

Правило Крамера.Используя определители, можно переписать формулы (3):

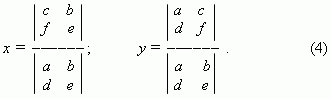
Формулы (4) называются правилом Крамера для системы двух линейных уравнений с двумя неизвестными.

П р и м е р . Решить систему уравнений

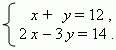
используя правило Крамера.

Р е ш е н и е . Здесь a = 1, b = 1, c = 12, d = 2, e = –3, f = 14 .

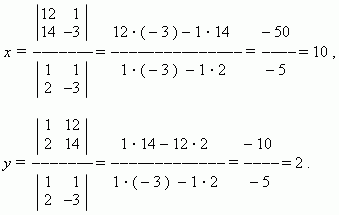
Исследование решений системы двух линейных уравнений с двумя неизвестными, показывает, что в зависимости от коэффициентов уравнений возможны три различных случая:

1) коэффициенты при неизвестных не пропорциональны: a : d ≠ b : e ,

в этом случае система линейных уравнений имеет единственное решение, получаемое по формулам (4);

2) все коэффициенты уравнений пропорциональны: a : d = b : e = c : f ,

в этом случае система линейных уравнений имеет бесконечное множество решений, так как здесь мы имеем фактически одно уравнение вместо двух.

П р и м е р . В системе уравнений

и эта система уравнений имеет бесконечное множество решений.

Разделив первое уравнение на 2, а второе – на 3, мы получим два

одинаковых уравнения:

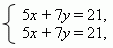
т.е. фактически одно уравнение с двумя неизвестными, у которого

бесконечное множество решений.

3) коэффициенты при неизвестных пропорциональны, но не пропорциональны свободным членам: a: d = b: e ≠ c: f,

в этом случае система линейных уравнений не имеет решений, так как мы имеем противоречивые уравнения.

П р и м е р . В системе уравнений

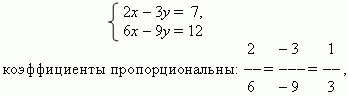
но отношение свободных членов 7 / 12 не равно 1 / 3.

Почему эта система не имеет решений? Ответ очень простой.

Разделив второе уравнение на 3, мы получим:

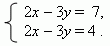
Уравнения этой системы противоречивы, потому что одно и то

же выражение 2x – 3y не может быть одновременно равно и 7, и 4.