Развертки кривых развертывающихся поверхностей

Развертки поверхностей

Представим поверхность в виде гибкой, но нерастяжимой пленки. Если при этом поверхность может быть совмещена с плоскостью без складок и разрывов, то она называется развертывающейся. Свойством развертываемости обладают многогранные поверхности и кривые линейчатые поверхности с ребром возврата, т.е. такие, которые образуются непрерывным движением прямой, касательной во всех своих положениях к некоторой кривой, называемой ребром возврата, это: торсы, конические и цилиндрические поверхности.

Плоская фигура, полученная в результате совмещения поверхности с плоскостью, называется разверткой. Между поверхностью и ее разверткой существует взаимно-однозначное точечное соответствие, т.е. каждой точке на поверхности соответствует единственная точка на развертке и наоборот. На развертке сохраняются длины линий, величины углов между кривыми (углом между кривыми называется угол между касательными к ним в точке пересечения) и площади фигур, ограниченных замкнутыми линиями. Из указанных свойств следует:

а) прямой линии на поверхности соответствует прямая на развертке;

б) прямым, параллельным на поверхности, соответствуют прямые, параллельные на развертке.

Однако оба указанных свойства обратной силы не имеют, т.е. не всякой прямой на развертке соответствует прямая на поверхности. Примерами этого могут служить цилиндрическая винтовая линия, параллели поверхности вращения.

Построение разверток поверхностей имеет большое практическое значение, так как развертки широко применяются при изготовлении изделий из листового материала путем изгибания.

Развертка поверхности многогранника

Развертка многогранника представляет собой плоскую фигуру, полученную при совмещении всех его граней с плоскостью. Следовательно, построение развертки многогранника сводится к определению размеров его граней, что, в свою очередь, связано с определением длин его ребер, которые являются сторонами многоугольников – граней. Ребра многоугольника условно разделяются на боковые и стороны основания.

Задача 15. Построить развертку поверхности наклонной трехгранной призмы ABCDEF (рис. 24).

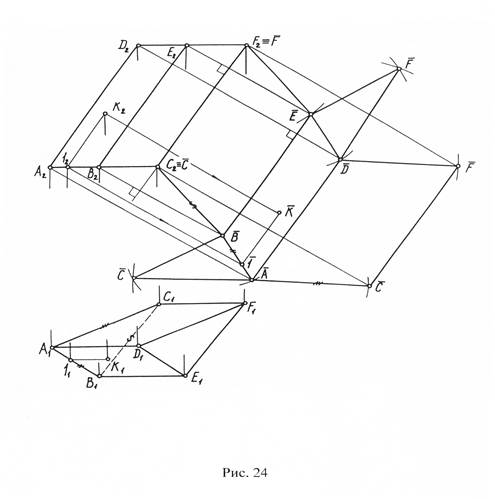
Наклонная призма изображена на рисунке 24. Призма расположена так, что ее боковые ребра параллельны плоскости П₂ и проецируются на нее в натуральную величину. Стороны основания призмы являются горизонталями и проецируются на плоскость П₁без искажения. Таким образом, длины сторон каждой грани известны, однако этого еще недостаточно определения формы и размеров боковых граней. Отбросим мысленно основания призмы и сделаем разрез по ребру CF. Приняв за плоскость развертки фронтальную плоскость, проходящую через ребро CF, совместим с ней последовательно боковые грани CFEB, BEDA, ADFC, поворачивая их соответственно вокруг ребер CF, BE, AD. Рассмотрим поворот грани CFEB вокруг ребра CF, приняв его за ось вращения:

1) точки C и F остаются неподвижными, т.е. /CF/=/C₂F₂/=/C^¯F^¯/, поворачиваются точки B и E, при этом их фронтальные проекции перемещаются соответственно по прямым, перпендикулярным C₂F₂;

2) для определения повернутого положения B^¯точки B из точки C₂≡ C^¯ проведем дугу радиуса R =/C₁B₁/, /CB/=/C₁B₁/ и сделаем засечку на этой прямой;

3) точку E^¯находим в пересечении прямой E₂E^¯ и дуги радиуса R =/F₁E₁/, /FE/=/ F₁E₁/;

4) соединив полученные точки C^¯, B^¯, E^¯ и F^¯, определяем форму и размеры грани CFEB;

5) ребро B^¯E^¯ принимается за ось вращения для грани BEDA.

Выполнив аналогичные построения при совмещении других граней призмы с фронтальной плоскостью, получим развертку боковой поверхности призмы, а, присоединив к ней оба основания, получим полную развертку призмы.

Для построения на развертке точки K(K₁,K₂), принадлежащей поверхности призмы, проведена прямая K1(K₁1₁, K₂1₂), параллельная боковым ребрам призмы, на развертке построена соответствующая ей прямая K^¯1^¯и на ней отмечена точка K^¯.

Если боковые ребра призмы не параллельны ни одной из плоскостей проекций, то для построения развертки такой призмы необходимо сначала построить ее ортогональную проекцию на плоскость, параллельную боковым ребрам призмы.

Развертки кривых развертывающихся поверхностей

Построение точных разверток кривых развертывающихся поверхностей сложно и, как правило, не вызывается практической необходимостью. Поэтому обычно строят приближенные развертки поверхностей, вполне пригодные для практических целей. Для построения развертки конической или цилиндрической поверхности в нее вписывают соответственно пирамидальную или призматическую поверхность, и развертку последней принимают за приближенную развертку заданной поверхности. Очевидно, чем больше граней у вписанной поверхности, тем точнее развертка. Исходя из этого, развертку конической или цилиндрической поверхности можно рассматривать как предел, к которому стремится развертка вписанной пирамидальной или призматической поверхности при неограниченном увеличении числа граней.

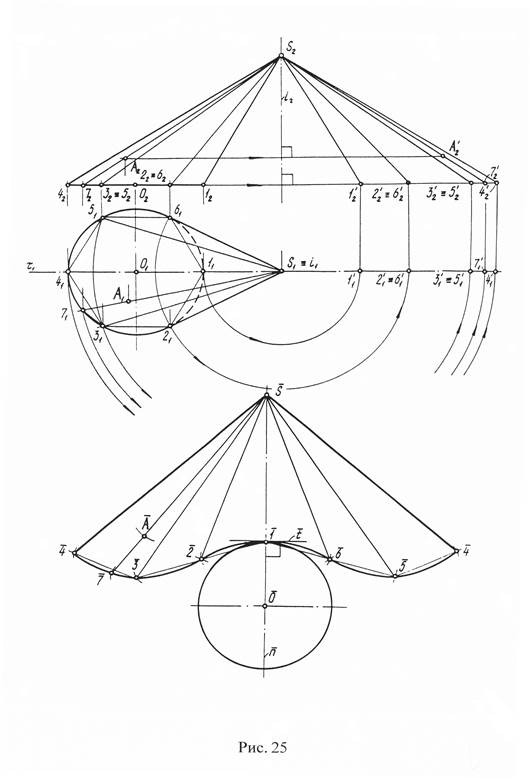
Задача 16. Построить развертку поверхности конуса (рис. 25).

Впишем в поверхность конуса шестигранную пирамиду с основанием в виде правильного шестиугольника и построим ее развертку.

Развертка боковой поверхности пирамиды будет состоять из шести треугольников, для построения которых нужно знать величину их сторон – ребер пирамиды. Величина сторон основания пирамиды определяется их горизонтальной проекцией. Длину боковых ребер находим поворотом вокруг оси i, проходящей через вершину пирамиды S и перпендикулярной к плоскости П₁. Фронтальные проекции повернутых до фронтального положения ребер (S₂ 1₂′, S₂ 2₂′ ≡ S₂ 6₂′, S₂ 3₂′ ≡ S₂ 5₂′, S₂ 4₂′) определяют их длину. Отметим, что боковая поверхность пирамиды симметрична относительно плоскости τ, в которой лежат ее самое длинное боковое ребро S4 и самое короткое S1. Относительно этих ребер развертка пирамиды также симметрична.

Построив развертку боковой поверхности пирамиды, соединяем точки 4^¯, 3^¯, 2^¯,1^¯, 6^¯, 5^¯, 4^¯ плавной кривой линией. Получаем приближенную развертку боковой поверхности конуса, пристроив к ней окружность основания, получим полную развертку поверхности конуса.

Для нанесения на развертке точки A^¯, соответствующей точке A поверхности конуса, через последнюю проведена образующая S7, а на развертке построена отвечающая ей прямая (S^¯7^¯) и на ней от точки S^¯отложена длина отрезка /SA/=/S₂A′₂/. При этом точка 7^¯ получена в пересечении кривой (4^¯ -3^¯ -2^¯ -1^¯ -6^¯ -5^¯ -4^¯ ) и дуги окружности с центром в точке 3^¯ и с радиусом R = / 3^¯ -7^¯ /=/ 3₁-7₁/.