Контакты

Случайная статья

Поверхности. Плоскость(поверхность первого порядка). Поверхности второго порядка. Цилиндры второго порядка. Поверхности вращение второго порядка

Стр 1 из 2Следующая ⇒

Поверхности

1. Плоскость(поверхность первого порядка)

Уравнение плоскостиAx+By+Cz+D=0

2. Поверхности второго порядка

2.1 Цилиндры второго порядка

Определение Цилиндрической поверхностьюназывается поверхность, описываемая прямой (образующей),движущейся вдоль некоторой линии (направляющей) и остающейся параллельной исходному направлению.

Определение Цилиндром второго порядканазывается цилиндрическая поверхность, направляющей которой является эллипс (окружность), гипербола или парабола.

Рассмотрим цилиндры второго порядка, у которых образующая параллельна оси Оz.

1) Эллиптический цилиндр (рисунок 10.5).

.

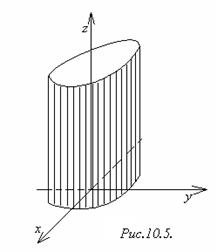
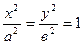В частности эллиптический цилиндр имеет в качестве направляющей окружность. Его уравнение

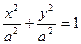или .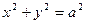

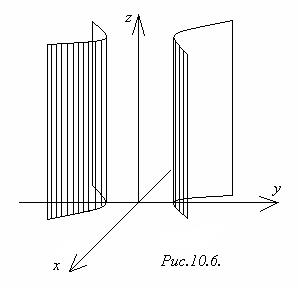
2) Гиперболический цилиндр (рисунок 10.6)

- .

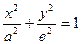3) Параболический цилиндр (рисунок 10.7).

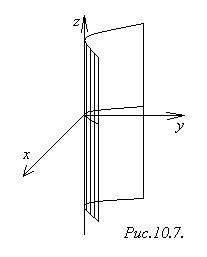х² = 2ру.

2.2 Поверхности вращение второго порядка

Определение 10.5. Поверхностью вращения второго порядканазывается поверхность, образованная вращением линии второго порядка её оси.

1) Эллипсоид вращения.При вращении эллипса 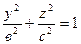, х = 0 вокруг оси Оz

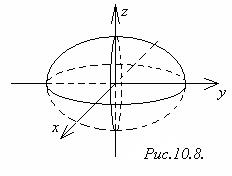
получим поверхность, которая называется

эллипсоидом вращения. 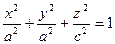(рисунок 10.8).

При а = с получаем сферу х² + у² + z² = a².

2) Однополостный гиперболоид образуется при вращении гиперболы ,

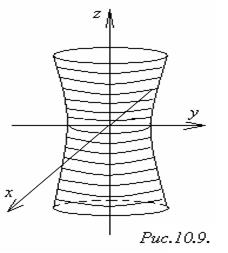х = 0 вокруг оси Оz.

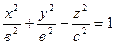(рисунок 10.9).

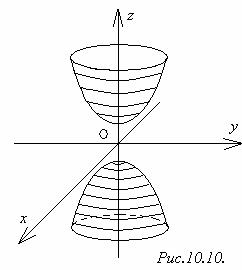3) Двуполостный гиперболоидобразуется при вращении гиперболы 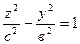, х = 0 вокруг оси Оz.

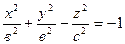(рисунок 10.10).

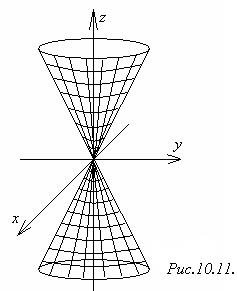4) Конус вращенияобразуется при вращении прямых , х = 0 вокруг оси Оz.

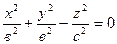(рисунок 10.11).

5) Параболоид вращенияполучается вращением параболы у² = 2рz , х = 0 вокруг оси Оz

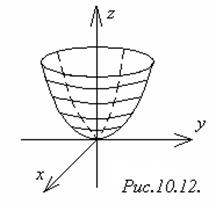х² + у² = 2рz или (рисунок 10.12).

12 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.