САМОСТОЯТЕЬНО

Лабораторная работа:

Построение поверхностей в трехмерном пространстве

Цель работы:Изучение графических возможностей пакета MS Excel. Приобретение навыков построения графика функции в трехмерном пространстве.

Задание 1. Построить верхнюю часть эллипсоида:

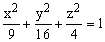
Для построения поверхности необходимо разрешить заданное уравнение относительно переменной z.

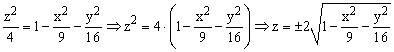
Так как в условии речь идет о верхней части эллипсоида, то рассмотрим ОДЗ положительной части уравнения:

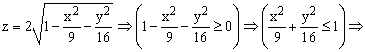
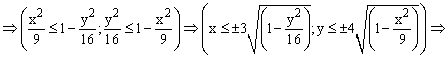
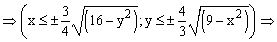
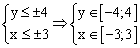
Приступим к построению поверхности. В диапазон B1:J1 введем последовательность значений переменной y: -4, -3, …, 4, а в диапазон ячеек А2:А14 последовательность значений переменой x: -3, -2,5, …, 3.

В ячейку В2 введем формулу =2*(1-($A2^2)/9-(B$1^2)/16)^0,5.

Знак $, стоящий перед буквой в имени ячейки, дает абсолютную ссылку на столбец с данным именем, а знак $, стоящий перед цифрой – абсолютную ссылку на строку с этим именем. Поэтому при копировании формулы из ячейки В2 в ячейки диапазона B2:J14 в них будет найдено значение z при соответствующих значениях x, y. Т.о. создается таблица значений z (см. рис. 1).

Перейдем к построению поверхности.

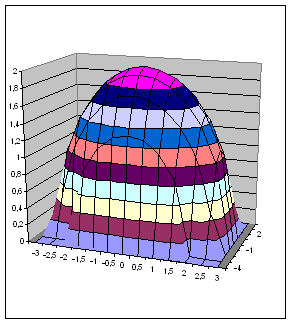
Выделим диапазон ячеек A1:J14, содержащий таблицу значений функции и ее аргументов, вызовем Мастер диаграмм и тип диаграммы Поверхность. После нажатия кнопки Готово получим изображение заданной поверхности (см. рис. 2).

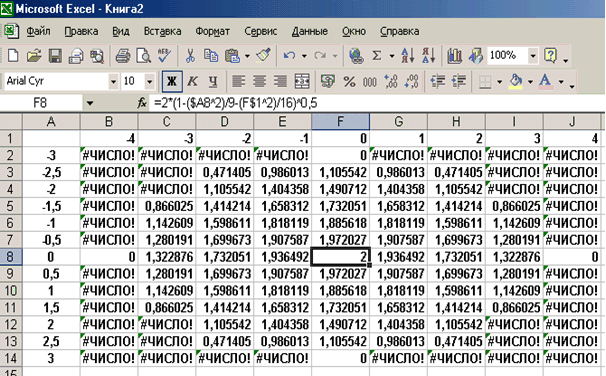
Рис. 1


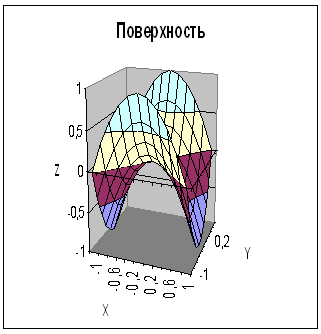
Рис. 2	Рис. 3

Задание 2. Построить поверхность z = x²-y² при x, y [-1;1].

В диапазон B1:L1 введем последовательность значений переменной x: -1, -0.8, …, 1, а в диапазон ячеек А2:А12 последовательность значений переменой y. В ячейку В2 введем формулу =$A2^2-B$1^2 и скопируем ее в ячейки диапазона B2:L12. На рис. 3. изображена заданная поверхность.

САМОСТОЯТЕЬНО

ЗАДАНИЕ. Построить эллиптический (четные варианты) или гиперболический (нечетные варианты) параболоид, заданный уравнением:

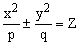
Знак "плюс" относится к уравнению эллиптического параболоида.
Знак "минус" к уравнению гиперболического параболоида.

№	p	q















	1.5	2.5
	2.5	1.5