
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Касательная плоскость
Поверхность
[править]
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Поверхность (значения).
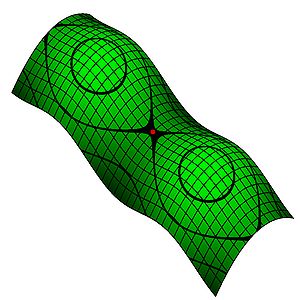

Пример простой поверхности
Пове́рхность — традиционное название для двумерного многообразия в пространстве.
Способы задания
Поверхность определяется как множество точек, координаты которых удовлетворяют определённому виду уравнений:
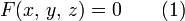
Если функция 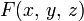 непрерывна в некоторой точке и имеет в ней непрерывные частные производные, по крайней мере одна из которых не обращается в нуль, то в окрестности этой точки поверхность, заданная уравнением (1), будет правильной поверхностью.
непрерывна в некоторой точке и имеет в ней непрерывные частные производные, по крайней мере одна из которых не обращается в нуль, то в окрестности этой точки поверхность, заданная уравнением (1), будет правильной поверхностью.
Помимо указанного выше неявного способа задания поверхность может быть определена явно, если одну из переменных, например z, можно выразить через остальные:
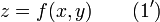
Также существует параметрический способ задания. В этом случае поверхность определяется системой уравнений:
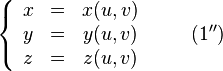
Понятие о простой поверхности
Интуитивно простую поверхность можно представить как кусок плоскости, подвергнутыйнепрерывным деформациям (растяжениям, сжатиям и изгибаниям).
Более строго, простой поверхностью называется образ гомеоморфного отображения (то есть взаимно однозначного и взаимно непрерывного отображения) внутренности единичного квадрата. Этому определению можно дать аналитическое выражение.
Пусть на плоскости с прямоугольной системой координат u и v задан квадрат, координаты внутренних точек которого удовлетворяют неравенствам 0 < u < 1, 0 < v < 1. Гомеоморфный образ квадрата в пространстве с прямоугольной системой координат х, у, z задаётся при помощи формул х = x(u, v), у = y(u, v), z = z(u, v) (параметрическое задание поверхности). При этом от функций x(u, v), y(u, v) и z(u, v) требуется, чтобы они были непрерывными и чтобы для различных точек (u, v) и (u', v') были различными соответствующие точки (x, у, z) и (x', у', z').
Примером простой поверхности является полусфера. Вся же сфера не является простой поверхностью. Это вызывает необходимость дальнейшего обобщения понятия поверхности.
Подмножество пространства, у каждой точки которого есть окрестность, являющаяся простой поверхностью, называется правильной поверхностью.
Поверхность в дифференциальной геометрии
В дифференциальной геометрии исследуемые поверхности обычно подчинены условиям, связанным с возможностью применения методов дифференциального исчисления. Как правило, это — условия гладкости поверхности, то есть существования в каждой точке поверхности определённой касательной плоскости, кривизны и т. д. Эти требования сводятся к тому, что функции, задающие поверхность, предполагаются однократно, дважды, трижды, а в некоторых вопросах — неограниченное число раз дифференцируемыми или даже аналитическими функциями. При этом дополнительно накладывается условие регулярности.
Случай неявного задания. Поверхность, заданная уравнением 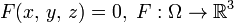 , является гладкой регулярной поверхностью, если
, является гладкой регулярной поверхностью, если 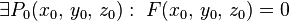 , функция
, функция 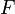 непрерывно дифференцируема в своей области определения
непрерывно дифференцируема в своей области определения 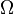 , а её частные производные одновременно не обращаются в нуль (условие правильности) на всём множестве
, а её частные производные одновременно не обращаются в нуль (условие правильности) на всём множестве 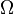 :
:
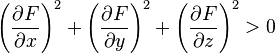
Случай параметрического задания. Зададим поверхность векторным уравнением 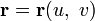 , или, что то же самое, тремя уравнениями в координатах:
, или, что то же самое, тремя уравнениями в координатах:
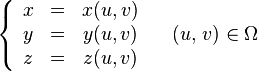
Эта система уравнений задаёт гладкую регулярную поверхность, если выполнены условия:
· система устанавливает взаимно однозначное соответствие между образом и прообразом 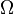 ;
;
· функции 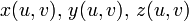 непрерывно дифференцируемы в
непрерывно дифференцируемы в 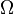 ;
;
· выполнено условие невырожденности:
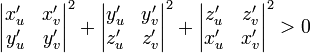
Геометрически последнее условие означает, что векторы 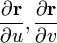 нигде не параллельны.
нигде не параллельны.
Параметры u, v можно рассматривать как внутренние координаты точек поверхности. Фиксируя одну из координат, мы получаем два семейства координатных кривых, покрывающих поверхность координатной сеткой.
Случай явного задания. Поверхность 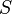 может быть определена как график функции
может быть определена как график функции 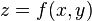 ; тогда
; тогда 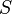 является гладкой регулярной поверхностью, если функция
является гладкой регулярной поверхностью, если функция 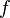 дифференцируема. Этот вариант можно рассматривать как частный случай параметрического задания:
дифференцируема. Этот вариант можно рассматривать как частный случай параметрического задания: 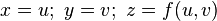 .
.
Касательная плоскость
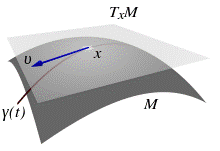

Касательная плоскость в точке поверхности.
Касательная плоскость в точке гладкой поверхности — это плоскость, имеющая максимальный порядоксоприкосновения с поверхностью в этой точке. Эквивалентный вариант определения: касательная плоскость есть плоскость, содержащая касательные ко всем гладким кривым, проходящим через эту точку.
Пусть гладкая кривая на параметрически заданной поверхности 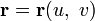 задана в виде:
задана в виде:
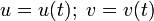 .
.
Направление 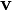 касательной к такой кривой даёт вектор:
касательной к такой кривой даёт вектор:
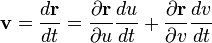
Отсюда видно, что все касательные ко всем кривым в данной точке лежат в одной плоскости, содержащей векторы 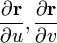 , которые мы выше предположили независимыми.
, которые мы выше предположили независимыми.
Уравнение касательной плоскости в точке 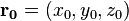 имеет вид:
имеет вид:
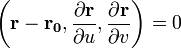 (смешанное произведение векторов).
(смешанное произведение векторов).
В координатах уравнения касательной плоскости для разных способов задания поверхности приведены в таблице:
касательная плоскость к поверхности в точке 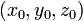
| |
| неявное задание | 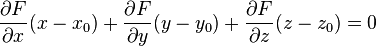
|
| явное задание | 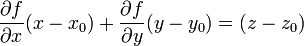
|
| параметрическое задание | 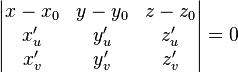
|
Все производные берутся в точке 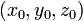 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|