Разработка тестовых заданий по математике (теоретический материал)

Разработка тестовых заданий по математике (теоретический материал)

Существуют различные классификации педагогических тестов. Одна из наиболее распространенных: 1) содержательно-ориентированные тесты; 2) критериально-ориентированные тесты.

Содержательно-ориентированный тест. Позволяет объективно дифференцировать испытуемых по уровню ЗУН, то есть главный результат тестирования – выявление места каждого учащегося относительно других учащихся, а не выявление того, достиг ли тестируемый определенного уровня усвоения учебного материала. Такой тест должен содержать задания разного уровня сложности и охватывать весь запланированный для проверки материал с учетом пропорционального соотношения различных разделов и тем. Задания разного уровня сложности имеют, как правило, разный «вес» как по их относительному числу в общей массе заданий, так и по оценочным баллам.

Критериально-ориентированный тест. Позволяет оценить, достиг ли учащийся определенного уровня усвоения учебного материала, в том числе минимально допустимого. Результаты тестирования каждого учащегося сравниваются не с результатами других учащихся, а с заранее заданным критерием уровня подготовленности. Такой тест может охватывать весь запланированный для проверки материал с учетом пропорционального соотношения различных разделов и тем (а может и не охватывать). При этом чаще всего тест состоит из однородных по типу и уровню сложности заданий. Все задания, как правило, оцениваются одинаковым числом баллов (обычно 1 балл за каждое правильно выполненное задание). Однако в некоторых случаях тест может включать небольшое число заданий повышенного уровня сложности.

Замечание. Часто встречаются тесты, выполняющие одновременно функции двух указанных выше видов тестов. Например, ЕГЭ по математике.

Формы тестовых заданий:

1) закрытая форма;

2) открытая форма;

3) задания на соответствие;

4) задания на установление правильной последовательности.

Задания закрытой формы имеют следующие характеристики и особенности:

1) в каждом задании предлагаются готовые ответы, только один из которых является правильным (4-5 ответов в задании);

2) все ответы должны быть правдоподобными и равнопривлекательными;

3) ошибка должна искусственно стимулироваться;

4) задания формулируются в виде утверждений, которые в зависимости от ответов учащихся превращаются в истинные или ложные высказывания.

Пример. Составить задание, которое проверяет умение учащихся находить наименьшее (наибольшее) значение функции на отрезке.

Возьмем функцию 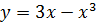и отрезок 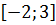. Сначала найдем правильный ответ.

Найдем производную данной функции: .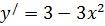

Получим, что 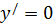при .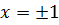

Найдем значения функции в точках 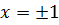и на концах отрезка :

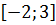Таким образом, получим .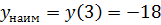

Теперь необходимо подобрать неправильные варианты ответов так, чтобы они учитывали типичные ошибки учащихся, «стимулировали» их делать эти ошибки.

Часто учащиеся находят не значения функции, а значения производной в точках: 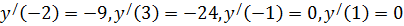. Итак, первый ошибочный вариант .

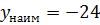Другой распространённой ошибкой является учет значений функции только в точках 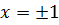, то есть 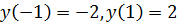. Значит, второй ошибочный вариант .

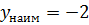Можно предположить, что некоторые ученики допустят следующую ошибку: выберут наименьшее из чисел -2, 3, -1, 1, а затем найдут значение функции при выбранном значении аргумента и получат .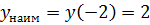

Осталось корректно сформулировать задание в виде утверждения, которое в зависимости от ответов учащихся превращается в истинное или ложное высказывание.

Наименьшее значение функции 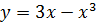на отрезке 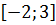равно

a) – 24;

b) – 18;

c) 2;

d) – 2.

Заметим, что формулировка задания в виде вопроса «Чему равно наименьшее значение функции 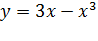на отрезке 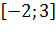?» или требования «Найти наименьшее значение функции 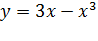на отрезке 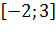» является некорректной.

Перед составлением теста по заданному разделу или теме школьного курса математики нужно составить его спецификацию. Для этого требуется выявить основные понятия, утверждения и типы задач, изученные в разделе или теме, а затем определить число заданий в тесте на каждое из этих понятий, утверждений и типов задач. Число заданий определяется распределением часов в учебной программе на разные части темы, а также значимостью понятия, утверждения или типа задач.

Задание 1. Составить спецификацию теста по теме «Логарифмическая функция» (учебник: Алимов Ш.А. и др. «Алгебра и начала математического анализа»). Предполагается, что тест будет использоваться в качестве контрольной работы по теме. Представить спецификацию в виде таблицы приведенного ниже вида (таблица 1).

Таблица 1. Спецификация теста по теме «Логарифмическая функция»

№	Понятие, утверждение, тип задачи	Число заданий
1.
2.
	Всего заданий

Комментарии к заданию:

- рекомендуется включить в спецификацию теста 15-20 заданий;

- рекомендуется планировать по 1-2 задания на каждое понятие, утверждение или тип задач (чаще 1, чем 2).

Задание 2. На основе созданной спецификации разработать два однотипных варианта критериально-ориентированного теста по теме «Логарифмическая функция». Каждый вариант должен состоять из 12-15 заданий закрытой формы базового уровня сложности и 3-5 заданий закрытой формы повышенного уровня сложности. Необходимо давать краткие пояснения по заданиям: как именно получены неправильные ответы к ним, какая ошибка в них заложена.

Комментарии к заданию:

- необходимо обращать особое внимание на подбор правдоподобных и равнопривлекательных ответов, используя, прежде всего, «стимулирование» типичных ошибок учащихся;

- при составлении заданий необходимо варьировать их условия (например, если в одном из заданий первого варианта дается логарифмическая функция с основанием 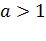, то в аналогичном задании второго варианта дается логарифмическая функция с основанием , и т.п.; также следует стремиться к разнообразию ситуаций внутри одного варианта).