Практическое занятие № 11. Виды динамических звеньев САР

Практическое занятие № 11. Виды динамических звеньев САР

По виду динамической характеристики элементы САР подразделяются на так называемые типовые динамические звенья:

· 1) усилительное звено (синонимы: безынерционное, пропорциональное, нулевого порядка);

· 2) апериодическое звено I порядка (инерционное);

· 3) интегрирующее звено (астатическое);

· 4) колебательное звено;

· 5) апериодическое звено II порядка;

· 6) дифференцирующее звено.

Усилительное звено (рис. 1)

Рис. 1. Усилительное звено Динамическая характеристика звена

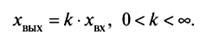(1)

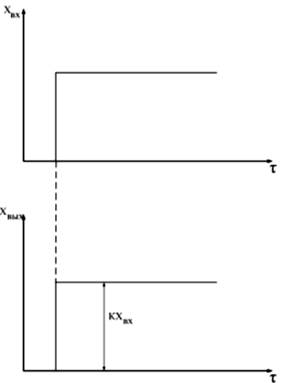
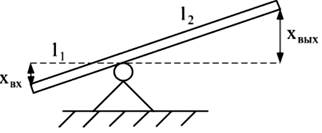
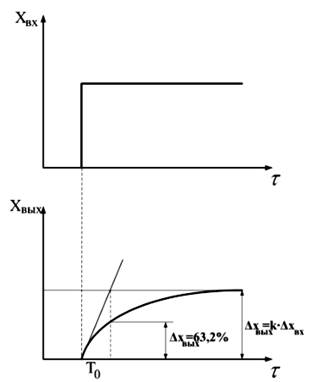
После нанесения скачком возмущения х_вх(τ) выходная величина х_вых(τ)) изменяется также скачком (рис. 2). Примеры: электронная лампа, редуктор, рычажное устройство (рис. 3).

Здесь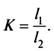


Рис. 2. Динамическая характеристика усилительного звена	Рис. 3. Рычажное устройство

Апериодическое звено 1-го порядка

Это звено, в котором может накапливаться или рассеиваться какой-либо вид материи или энергии, поданной на вход звена. В результате сигнал, поданный на вход звена, вызывает изменение выходной величины с некоторым замедлением. Это звено эквивалентно звену с самовыравниванием (рис. 4):

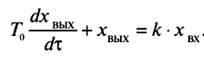(2)

Решением уравнения является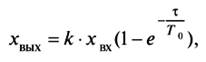

Эти постоянные коэффициенты зависят от конструкции и принципа действия звена.

Время разгона (3—4) Т₀ — это время, за которое х_ВЬ1Х достигнет 99% максимального значения. Представителем данного типа звена является, например, термопара. Ее уравнение имеет вид

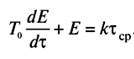(3)

Здесь Е — ТЭДС; 0_ср — температура измеряемой среды.

Интегрирующее звено (астатическое) (рис. 5)

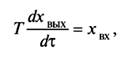(4)

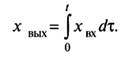(5)


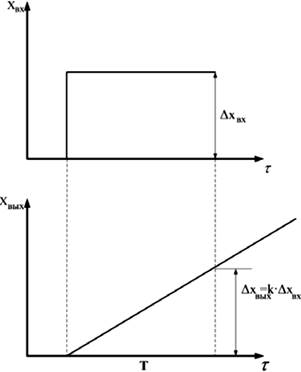
Рис. 4. Динамическая характеристика апериодического звена 1-го порядка	Рис. 5. Динамическая характеристика интегрирующего звена Здесь Т — время разгона объекта.

В отличие от апериодического звена величина х_ВЬ1Х с течением времени у интегрирующего звена не принимает нового установившегося значения (если нет физических ограничений).

Пример 1

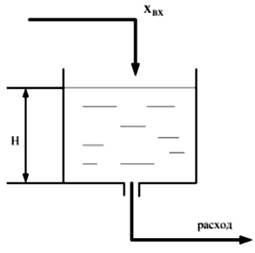
При скачке х_вх уровень Н растет, пока не будет переполнения (рис. 6). Это может быть в том случае, если выходное отверстие засорилось либо на трубопроводе после емкости установлен насос постоянной производительности. Возрастающее гидростатическое давление жидкости не влияет на производительность насоса.

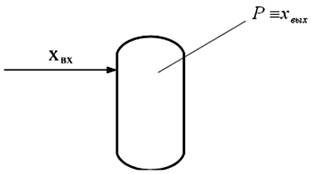
Пример 2

Непроточная емкость (физическое ограничение — механическая прочность баллона) (рис. 7).

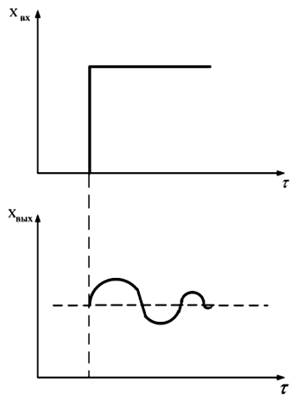
Колебательное звено

После скачкообразного изменения х_вх (рис. 8) изменение х_вых имеет форму затухающих синусоидальных колебаний (а — коэффициент затухания,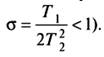


Рис. 6	Рис. 7

Звено описывается обыкновенным дифференциальным уравнением 2-го порядка:

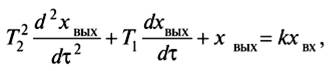(5)

Где Т₁, Т₂, k — постоянные коэффициенты.


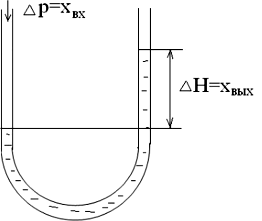
Рис. 8. Динамическая характеристика колебательного звена	Рис. 9

Решение уравнения имеет вид (7)

Где

	(8)
	(9)
	(10)
	(11)

В зависимости от значения о величина х_ВЬ1Х может совершать незатухающие колебания (о = 0), возрастающие колебания (а < 0), затухающие колебания (а < 1). Примером звена (а < 1) является U-образная трубка (рис. 9).

Апериодическое звено 2-го порядка

Зависимость х_ВЬ1Х =/(х_вх) в неустановившемся режиме для данного типа звена имеет вид 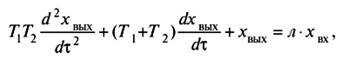(12)

Решением данного уравнения является

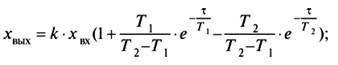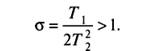(13) (14)

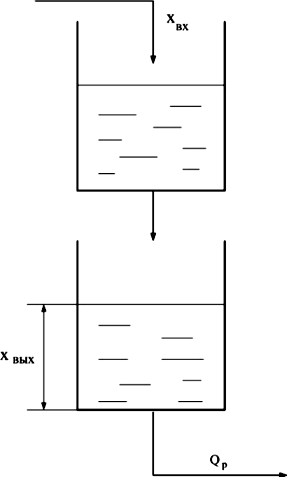
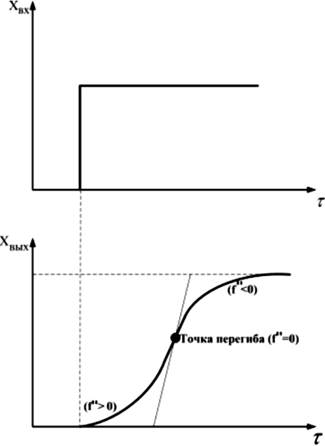
Величина х_ВЬ1Х с течением времени стремится к новому установившемуся значению без колебаний. Есть точка перегиба (рис. 10, 11).

Пример


Рис. 10. Двухъемкостный объект	Рис. 11. Динамическая характеристика двухъемкостного объекта

Уравнения колебательного и апериодического звена 2-го порядка имеют одинаковый вид. Как их отличить?

Пример:

(15)

Если а > 4 а₀, то это апериодическое звено 2-го порядка.

Если а > 4а₀, то это колебательное звено (так как здесь 4² < 4 -7).

Дифференцирующее звено

У звена такого типа изменение х_вых пропорционально скорости изменения х_вх (рис. 12—14).

1. Идеальное дифференцирующее звено 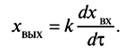(16)

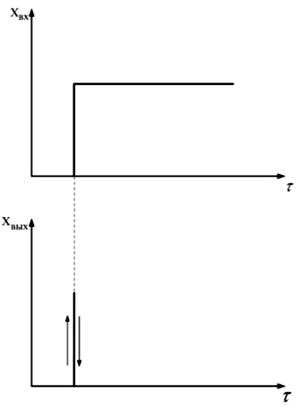
Рис. 12. Идеальное дифференцирующее звено

Величина x_вых в момент изменения х_вх меняется от 0 до max и снова возвращается к нулю.

2. Реальное дифференцирующее звено

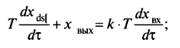(17)

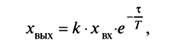(18)

Где Т — постоянная времени.

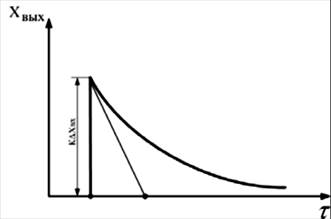
	Пример: Конденсатор С зарядили мгновенно. Затем он постепенно разряжается через сопротивление R.
Рис. 13. Реальное дифференцирующее звено	Рис. 14