Корень n-ой степени.. Корень n-ой степени, n - четное число.. Свойства функции корень n-ой степени при четных n.. Корень n-ой степени, n - нечетное число.

Стр 1 из 2Следующая ⇒

Корень n-ой степени.

Рассмотрим основную элементарную функцию, которая задается формулой 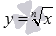, где n – натуральное число, большее единицы.

Корень n-ой степени, n - четное число.

Начнем с функции корень n-ой степени при четных значениях показателя корня n.

Для примера приведем рисунок с изображениями графиков функций 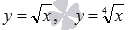и 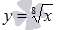, им соответствуют черная, красная и синяя линии.

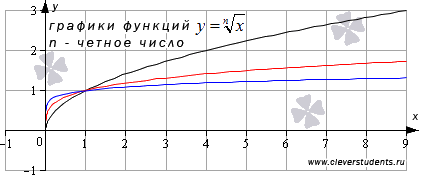
Аналогичный вид имеют графики функций корень четной степени при других значениях показателя.

Свойства функции корень n-ой степени при четных n.

· Область определения: множество всех неотрицательных действительных чисел .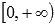

· При x=0 функция 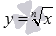принимает значение, равное нулю.

· Эта функция общего вида (не является четной или нечетной).

· Область значений функции: .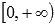

· Функция 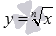при четных показателях корня возрастает на всей области определения.

· Эта функция имеет выпуклость, направленную вверх, на всей области определения, точек перегиба нет.

· Асимптот нет.

· График функции корень n-ой степени при четных n проходит через точки (0,0) и (1,1).

Корень n-ой степени, n - нечетное число.

Функция корень n-ой степени с нечетным показателем корня n определена на всем множестве действительных чисел. Для примера приведем графики функци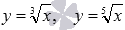й и 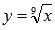, им соответствуют черная, красная и синяя кривые.

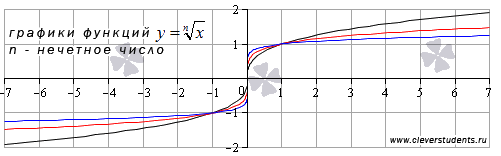
При других нечетных значениях показателя корня графики функции 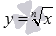будут иметь схожий вид.

12 Следующая ⇒