Равенство матриц.. A=B, если порядки матриц A и B одинаковы и aij=bij (i=1,2,.,m; j=1,2,.,n). Действия над матрицами.

ВОПРОСЫ К ЭКЗАМЕНУ ПО МАТЕМАТИКЕ (2019-20 уч. г.)

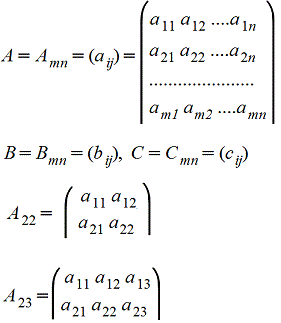24) Матрицы. Действия над матрицами.

Матрицей A=A_mn порядка m*n называется прямоугольная таблица чисел, содержащая m - строк и n – столбцов. Элементы матрицы a_ij,у которых i=j, называются диагональными и образуют главную диагональ.

Для квадратной матрицы (m=n) главную диагональ образуют элементы a₁₁, a₂₂,..., a_nn .

Равенство матриц.

A=B, если порядки матриц A и B одинаковы и aij=bij (i=1,2,...,m; j=1,2,...,n)

Действия над матрицами.

Сложение матриц - поэлементная операция. Суммой матрицы А и В называется такая матрица С, элементы которой равны сумме соответствующих элементов матриц А и В.

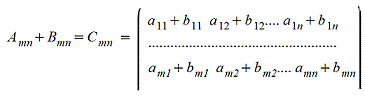
Вычитание матриц - поэлементная операция.

Произведение матрицы на число- поэлементная операция.

Умножение матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)

Возведение в степень

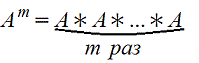
m>1 целое положительное число. А - квадратная матрица (m=n) т.е. актуально только для квадратных матриц

Транспонирование матрицы А. Транспонированную матрицу обозначают A^T или A'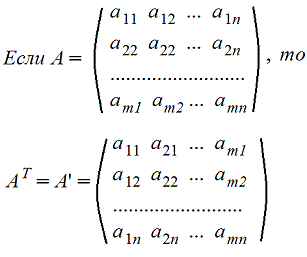

25) Определители матрицы второго и третьего порядка, способы их вычисления. Основные свойства определителей.

Матрицей второго порядка называется таблица

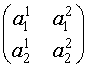составленная из элементов a₁¹, a₁², a₂¹, a₂².

Пары элементов a₁¹, a₁² и a₂¹, a₂² образуют строки матрицы, а пары a₁¹, a₂¹ и a₁², a₂² – столбцы.

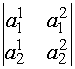Число (a₁¹·a₂² - a₁²·a₂¹), составленное из элементов матрицы (*), называют определителем второго порядка и обозначают

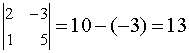
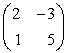Таким образом, чтобы сосчитать определитель второго порядка, надо перемножить элементы, стоящие на главной диагонали и вычесть произведение элементов, стоящих на побочной диагонали, например, определитель матрицы равен

Матрицей третьего порядка называется таблица, составленная из девяти элементов.

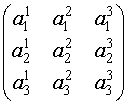
Матрица, имеющая одинаковое число строк и столбцов, называется квадратной, а число ее строк (столбцов) называется порядком матрицы.

Говорят, что элементы a₁¹, a₂², a₃³ образуют главную диагональ, а a₁³, a₂², a₃¹ – побочную.

определителем третьего порядка называется число, равное сумме

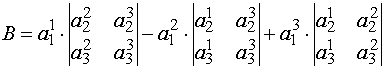. Это выражение называется разложением определителя по элементам первой строки.

Свойства определителей

Свойство 1. Величина определителя не изменяется при замене строк столбцами.

Свойство 2. При перестановке двух строк (столбцов) между собой, величина определителя меняет знак.

Свойство 3. Определитель с двумя одинаковыми (пропорциональными) строками (столбцами) равен нулю.

Свойство 4. Если все элементы некоторой строки (столбца) содержат одинаковый множитель, то этот множитель можно вынести за знак определителя.

Свойство 5. Если все элементы некоторой строки (столбца) есть сумма равного числа слагаемых, то определитель будет равен сумме определителей, в которых элементы указанной строки (столбца) записываются отдельными слагаемыми.

Свойство 6. Если все элементы некоторой строки (столбца) равны нулю, то весь определитель тоже равен нулю.

Свойство 7. Величина определителя не изменится, если к элементам некоторой строки (столбца) добавить соответствующие элементы другой строки(столбца), предварительно умножив их на один и тот же множитель.

26) Системы линейных алгебраических уравнений и их виды. Матричная запись систем линейных уравнений.

Системой линейных алгебраических уравнений (СЛАУ) называется система вида:

Упорядоченный набор значений 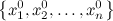называется решением системы, если при подстановке в уравнения все уравнения превращаются в тождество.

Виды СЛАУ

· СЛАУ называется совместной, если она имеет, хотя бы одно решение. В противном случае система называется несовместной.

· Система называется определённой, если она совместна и имеет единственное решение. В противном случае (т.е. если система совместна и имеет более одного решения) система называется неопределённой.

· Система называется однородной, если все правые части уравнений, входящих в нее, равны нулю одновременно.

· Система называется квадратной, если количество уравнений равно количеству неизвестных.

Матричная запись СЛАУ

Исходную СЛАУ можно записать в матричном виде:

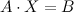где матрица 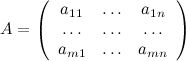называется матрицей системы, это матрица, составленная из коэффициентов при неизвестных; 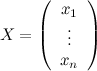- вектором-столбцом неизвестных, 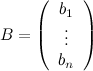- вектором-столбцом правых частей или свободных коэффициентов.

Пример. Систему нужно записать в матричной форме и выписать все матрицы, которые ей соответствуют.

Решение. Заданную СЛАУ записываем в матричной форме 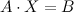, где матрица системы:

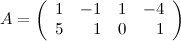
вектор-столбец неизвестных:

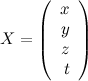
вектор-столбец свободных коэффициентов:

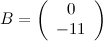
то есть, запись СЛАУ в матричной форме:

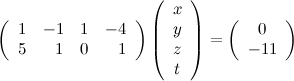
27) Элементарные преобразования расширенной матрицы системы линейных уравнений. Метод Гаусса.

Элементарными преобразованиями строк называют:

· перестановку местами любых двух строк матрицы;

· умножение на ненулевую константу любой строки матрицы;

· прибавление к любой строке матрицы другой строки, умноженной на ненулевое число.

Аналогично определяются элементарные преобразования столбцов.

А∙Х=В - матричная запись системы.

Расширенной матрицей

системы называется матрица Т,

полученная из матрицы системы

дописыванием справа после

вертикальной черты столбца свободных

членов.

Метод Гаусса

Метод Гаусса состоит из двух этапов:

«Прямой ход» - с помощью элементарных преобразований привести расширенную матрицу системы линейных алгебраических уравнений к «треугольному» ступенчатому виду: элементы расширенной матрицы, расположенные ниже главной диагонали, равны нулю (ход «сверху-вниз»). Например, к такому виду: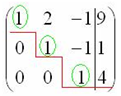

Для этого выполним следующие действия:

1) Пусть мы рассматриваем первое уравнение системы линейных алгебраических уравнений и коэффициент при х₁ равен К. Второе, третье и т.д. уравнения преобразуем следующим образом: каждое уравнение (коэффициенты при неизвестных, включая свободные члены) делим на коэффициент при неизвестном х₁, стоящий в каждом уравнении, и умножаем на К. После этого из второго уравнения (коэффициенты при неизвестных и свободные члены) вычитаем первое. Получаем при х₁ во втором уравнении коэффициент 0. Из третьего преобразованного уравнения вычитаем первое уравнение, так до тех пор, пока все уравнения, кроме первого, при неизвестном х₁ не будут иметь коэффициент 0.

2) Переходим к следующему уравнению. Пусть это будет второе уравнение и коэффициент при х₂ равен М. Со всеми «нижестоящими» уравнениями поступаем так, как описано выше. Таким образом, «под» неизвестной х₂ во всех уравнениях будут нули.

3) Переходим к следующему уравнению и так до тех пора, пока не останется одна последняя неизвестная и преобразованный свободный член.

«Обратный ход» метода Гаусса – получение решения системы линейных алгебраических уравнений (ход «снизу-вверх»).Из последнего «нижнего» уравнения получаем одно первое решение – неизвестную х_n. Для этого решаем элементарное уравнение А*х_n = В

Пример.

Решим систему линейных уравнений методом Гаусса, как советуют некоторые авторы:

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

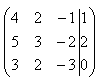
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Поступим так:
1 шаг. К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.

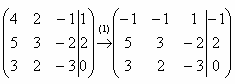
Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное действие: умножить первую строку на –1 (сменить у неё знак).

Дальше алгоритм работает уже по апробированной методике:

2 шаг. Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.

3 шаг. Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.

4 шаг. К третьей строке прибавили вторую строку, умноженную на 2.

5 шаг. Третью строку разделили на 3.

Признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде (0 0 11 |23), и, соответственно, 11x₃ = 23, x₃ = 23/11, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.

Выполняем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает «снизу вверх». В данном примере получился подарок:

x₃ = 1
x₂ = 3
x₁ + x₂ – x₃ = 1, следовательно x₁ + 3 – 1 = 1, x₁ = –1

Ответ: x₁ = –1, x₂ = 3, x₃ = 1.