РАЗДЕЛ 8. НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА

РАЗДЕЛ 8. НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА

ТЕМА: Понятие о производной функции. Приращение функции

Цель занятия: дать определение производной; научиться вычислять приращение функции.

Порядок выполнения работы:

1)Изучить теоретический материал, составить конспект в тетради;

2) В течение пары выполнить задания по материалу лекции (решить в тетради и выслать фотографии или документ преподавателю в социальной сети или на личную почту);

Контакты преподавателя: Arina_Kozlova96@mail.ru; https://vk.com/rina1996

ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ ДЛЯ САМОСТОЯТЕЛЬНОГО ИЗУЧЕНИЯ

Изучая поведение функции y=f(x) около конкретной точки x₀, важно знать, как меняется значение функции при изменении значения аргумента. Для этого используют понятия приращений аргумента и функции.

Пусть функция y=f(x) определена в точках x₀ и x₁. Разность x₁−x₀ называют приращением аргумента(при переходе от точки x₀ к точке x₁), а разность f(x₁)-f(x₀) называют приращением функции.

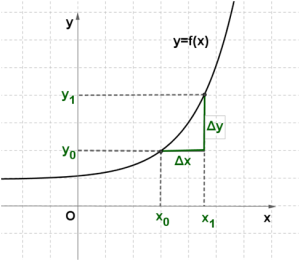
Приращение аргумента обозначают Δx (читают: дельта икс; Δ — прописная буква греческого алфавита "дельта"; соответствующая строчная буква пишется так: δ). Приращение функции обозначают Δy или Δf.

Итак, x₁-x₀=Δx, значит, x₁=x₀+Δx.

f(x₁)-f(x₀)=Δy, значит,

Δy=f(x0+Δx)-f(x0) (1)

Рассмотрим пример:

Пример 1.

Найдем приращение Δx и Δf в точке x_0,если f(x)= x², x₀=2 и х=1,9

Решение:

Δx = x₁−x₀= 1,9-2 = -0,1

Δf = f(1,9) –f(2) = 1,9²-2²= -0,39

Ответ: Δx = -0,1; Δf = -0,39

ПРАКТИЧЕСКИЕ ЗАДАНИЯ

Задание 1. Найти приращение Δx и Δf в точке x_0,если f(x)= x², x₀=2 и х=2,1

Задание 2. Найти приращение функции 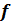в точке ,
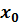если f(x)=2x²−3, x₀=3, △x= −0,2

△f =_______________

Задание 3. Найти приращение функции 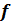в точке ,
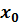если f(x)=2x+1; x₀= 5; △x= − 0,01

△f =_______________

Задание 4. Найти приращение функции 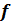в точке ,
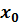если f(x)=2x−3; x₀=−2; △x=0,1

△f =_______________

Задание 5. Найти приращение функции 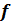в точке ,
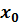если f(x)=0,5² * x; x₀=−2; △x=0,1

△f =_______________

Задание 6. Найти приращение функции 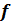в точке ,
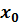если f(x)= 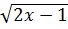; x₀=1,22; x =1,345

△f =_______________