Глава 1. Теория выпуклого программирования

Введение

В данной курсовой работе будет рассмотрено приближённое решение задач

выпуклого программирования методом кусочно-линейной аппроксимации.

Глава 1. Теория выпуклого программирования

Пусть С - не пустое выпуклое множество Х. Функция f(x), определенная

на С, называется выпуклой, если для всех x, yϵC, αϵ0, 1 выполняется неравенство

f (αx+(1-α)y)≤αf (x)+(1-α)f (y). (1.1)

Если при любых х≠у и 0<α<1 имеет место строгое неравенство, то

функция f(x) называется строго выпуклой. По определению: f(x) вогнута

(строго вогнута) на С, если - f(x) выпукла (строго выпукла) на С.

Понятие выпуклости может быть обобщено на случай, когда область

определения функции f(x) является множеством производной природы.

Функцию f(x)ϵ{X→R}, определённую на выпуклом множестве МᴄX, называются

выпуклой на М, если для произвольных х, уϵМ и αϵ0, 1 выполняется

неравенство (1.1). Если (1.1) при х≠у и 0<α<1 выполняется строго, то f(x)

называется строго выпуклой на М. Если в (1.1) знак ≤ заменить на ≥, то

получим определение вогнутой (соответственно строго вогнутой)

функции на М.

Будем говорить, что f(x) выпукла (вогнута), если f(x) выпукла (вогнута)

на М=Х.

Легко проверяется следующее свойство выпуклых на М функций:

1. Если f(x) выпукла на М, то множество

{xϵM: f (x)≤α}

либо пусто, либо выпукло при любом αϵR.

2. Если функция {f_i (x): i=1,..., m} выпуклы на М, то функция

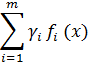
выпукла на М при любых γ_i≥0 (i=1,...,m).

3. Из выпуклости функции f(x) на М следует

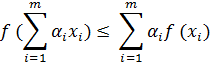
для любых конечных совокупностей

{x_i}ᴄM, здесь α_i≥0 (i=1,..., m), .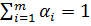

4. Функция f(x) выпукла тогда и только тогда, когда

g (t)=f (x+ts)

выпукла на R при любых x, sєX.

Введём понятие надграфика (epi f) выпуклой на М функции:

epi f={[x,μ]: f (x)≤μ, xϵM}.

Непосредственно проверяется:

5. Функция f(x), определённая на М, выпукла на М тогда и только тогда, когда

множество epi f выпукло.

Определим с-внутренность (ядро) выпуклого множества МᴄХ. Точка хєМ

называется с-внутренней, если для любого уєХ найдётся t₀>0 такое, что

x+tyϵM

для всех 0<t<t₀.