Описание метода измерений

Работа № 15

Изучение вязкости воздуха

Цель: определение коэффициента вязкости воздуха и исследование зависимости объёма воздуха, протекающего через капилляр, от его размеров.

Оборудование: набор капилляров, стеклянный баллон, насос, манометр, барометр, секундомер.

Описание метода измерений

Явления переноса – это процессы установления равновесия в системе путём переноса массы (диффузия), энергии (теплопроводность) и импульса молекул (внутреннее трение или динамическая вязкость).

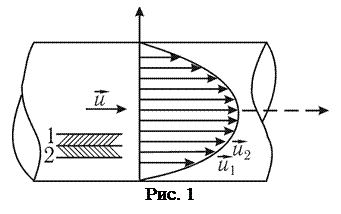В явлении вязкости наблюдается перенос импульса от более быстрых участков потока к менее быстрым. При течении газа или жидкости, например внутри трубы, скорости слоев различны: их распределение при ламинарном течении показано на рис. 1 (длина стрелки показывает скорость данного слоя). Причиной этого является хаотическое тепловое движение молекул, при котором они непрерывно переходят из слоя в слой и в соударениях с другими молекулами обмениваются импульсами. Так, молекулы второго слоя, попадая в слой 1, переносят свой импульс направленного движения , а в слой 2 приходят молекулы с меньшим импульсом . В результате второй слой тормозится, а первый – ускоряется. Опыт показывает, что импульс dp, передаваемый от слоя к слою через поверхность S, пропорционален градиенту скорости du/dx, площади S и времени переноса dt:

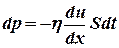В результате между слоями возникает сила внутреннего трения (закон Ньютона)

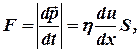(1)

где h – коэффициент вязкости среды.

Для идеального газа коэффициент вязкости

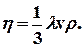(2)

Средняя длина свободного пробега молекул

, (3)

где k= 1,38×10^–23 Дж/К – постоянная Больцмана,

d – эффективный диаметр молекул (для воздуха d@ 4×10^–10 м),

Т, Р – температура и давление газа.

Средняя скорость теплового движения молекул

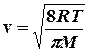, (4)

где R= 8,31 Дж/моль×К – универсальная газовая постоянная,

М – масса одного моля газа (для воздуха М = 28,9 г/моль).

Плотность газа согласно уравнению состояния идеального газа

. (5)

При ламинарном течении через трубу круглого сечения радиусом r (капилляр) и длиной L за время t протекает газ или жидкость, объём Vкоторых определяется по формуле Пуазейля:

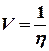
, (6)

где DР – разность давлений на концах капилляра.

Если в баллоне создать избыточное над атмосферным Р₀ давление

DР= Р – Р₀ = r_жgh (r_ж – плотность жидкости в манометре, h – разность уровней жидкости) и соединить капилляр с атмосферой, то за время dt через капилляр вытечет некоторое количество воздуха, масса которого

dm= rdV, (7)

где r – плотность воздуха в капилляре, зависящая (см. формулу (5)) от давления воздуха, dV – объём вышедшего воздуха.

Давление воздуха в капилляре изменяется от Р₀ до Р₀ + rgh, но так, как
rgh<< Р₀, то с достаточной точностью можно принять давление воздуха в капилляре равным атмосферному Р₀. Тогда плотность воздуха (из уравнения Менделеева–Клапейрона)

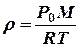. (8)

Объём воздуха dV, прошедшего через капилляр за время dt, описывается формулой Пуазейля (6):

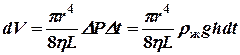, (9)

а масса воздуха, вытекающего из баллона, с учётом формул (8) и (9)

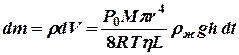. (10)

Из уравнения состояния идеального газа выразим изменение массы газа dm в баллоне через уменьшение давления в нём.

Так как dP= r_жgdh, то

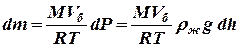. (11)

Исключая dmиз уравнений (10) и (11), получаем

. (12)

Решая это дифференциальное уравнение при условии, что за время опыта давление в баллоне уменьшится от r_жgh₀ до r_жgh, получаем

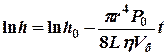. (13)*

Таким образом, формула (13) связывает разность давлений h на концах капилляра с временем t истечения воздуха, его вязкостью h и размерами капилляра r и L.

12 Следующая ⇒