Тема урока: Физический и геометрический смысл производной. Касательная к графику функции.

Тема урока: Физический и геометрический смысл производной. Касательная к графику функции.

Ход урока

“Человек лишь там чего – то добивается, где он верит в свои силы”

Л. Фейербах

Устный счет

1. Найдите производные:

( ) ' ( ) ' ( )'

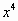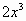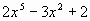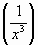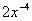', ( )' , (4sin x)', (cos2x)', (tg x)', '

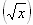2. Логический тест.

а) Вставить пропущенное выражение.

5х³-6х	15х²-6	30х
2sinx	2cosx…
cos2x	… …

Изучение нового материала.

Пойдем по пути Ньютона и Лейбница и посмотрим, каким способом можно анализировать процесс, рассматривая его как функцию времени.

Введем несколько понятий, которые помогут нам в дальнейшем.

Графиком линей ной функции y=kx+ b является прямая, число k называют угловым коэффициентом прямойk=tg 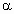, где 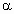– угол прямой, то есть угол между этой прямой и положительным направлением оси Ох.

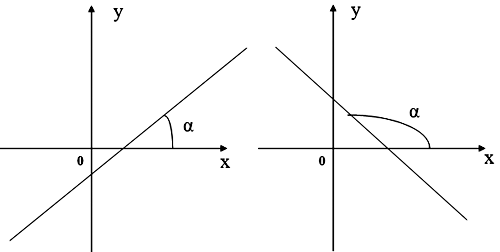
Рисунок 1

Рассмотрим график функции у=f(х). Проведем секущую через любые две точки, например, секущую АМ. (Рис.2)

Угловой коэффициент секущей k=tg 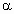. В прямоугольном треугольнике АМС <МАС = 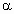(объясните почему?). Тогда tg 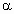= = 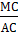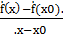, что с точки зрения физики есть величина средней скорости протекания любого процесса на данном промежутке времени, например, скорости изменения расстояния в механике.

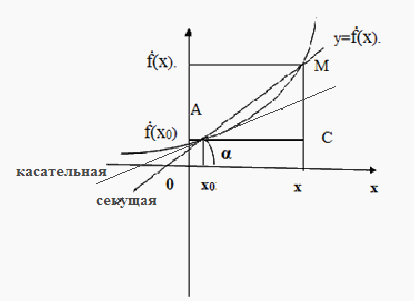
Рисунок 2

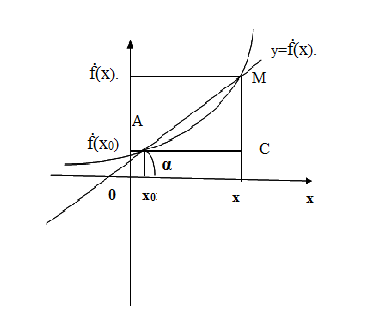
Рисунок 3

Сам термин “скорость” характеризует зависимость изменения одной величины от изменения другой, и последняя необязательно должна быть временем.

Итак, тангенс угла наклона секущей tg = .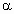

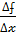Нас интересует зависимость изменения величин в более короткий промежуток времени. Устремим приращение аргумента к нулю. Тогда правая часть формулы – производная функции в точке А (объясните почему). Если 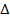х –> 0, то точка М движется по графику к точке А, значит прямая АМ приближается к некоторой прямой АВ, которая является касательной к графику функции у = f(х) в точке А. (Рис.3)

Угол наклона секущей стремится к углу наклона касательной.

Геометрический смысл производной состоит в том, что значение производной в точке равно угловому коэффициенту касательной к графику функции в точке.

Механический смысл производной.

Тангенс угла наклона касательной есть величина, показывающая мгновенную скорость изменения функции в данной точке, то есть новая характеристика изучаемого процесса. Эту величину Лейбниц назвал производной, а Ньютон говорил, что производной называется сама мгновенная скорость.

III. Решение заданий.

Угловой коэффициент касательной к кривой f(х) = х³ в точке х₀ – 1 есть значение производной этой функции при х = 1. f’(1) = 3х²; f’(1) = 3.

Ответ: 3.