Определение производной.. Обозначение производной: .. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ. II. Решение упражнений.

Определение производной.

Производной функции y = f(x) в данной точке x₀ называется предел отношения приращения функции в этой точке к приращению аргумента, при условии, что приращение аргумента стремится к нулю.

Обозначение производной: .

- Где в жизни применяется понятие производной? В физике – это скорость, ускорение, работа; в математике – это исследование различных функций при практических расчетах в автомобилестроении, судостроении, электронике и т.д.

Операция вычисления производной называется дифференцированием.

ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ

Карточка 1	Карточка 2	Карточка 3	Карточка 4
Для данной функции найдите предел отношения приращения функции к приращению аргумента при Δx 0
у = –3х + 1	у = 5х + 1	у = –4х – 1	у = 7х – 2

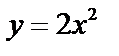
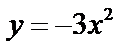
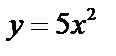
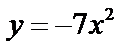
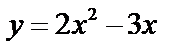
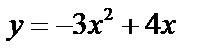
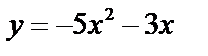
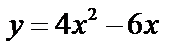
II. Решение упражнений.

1. По определению найти производную функции:

а) у = 3х² – 4х + 5 в точке х₀ = 2, в) у = х – 2х³,

б) у = х³ + 3х², г) у = 4х³ + 5х² – 7х – 4.

2. Тело, масса которого m = 5 кг, движется прямолинейно по закону s = l – t + t². Найти кинетическую энергию тела через 10 с после начала движения.

3. Самостоятельно.

Вариант 1	Вариант 2
1. По определению найти производную функции:
а) у = 5х,	а) у = 2х,
б) у = 2х – 1,	б) у = 3х + 2,
в) у = -3х³ + 2,	в) у = 3 – 2 х³,
г) у = 2х³– 3х² + 5х – 3.	г) у = 4х²– 3х³ + 5 – 3х.

⇐ Предыдущая 12