Хелпикс

Главная

Контакты

Случайная статья



Тема. Решение рациональных неравенств. Метод интервалов.



Тема. Решение рациональных неравенств. Метод интервалов.

 Примеры. Решить неравенство:

1. 2х – 8 > 0

2x > 8 │: 2 при делении на положительной число знак нер.не меняется

x > 4

Ответ: (4; + ∞)

2. 8 – 3х ≤ 12

 – 3х ≤ 12 – 8

– 3х ≤ 4 │: (- 3) при делении на отрицательное число знак нер. меняется на противоположный и выделяем целую часть, получим:

х 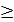 - 1

Ответ: [- 1 ; + ∞)

Неравенства степенью выше единица, в том числе и дробно-рациональные решаются методом интервалов

3.Ре­ши­те не­ра­вен­ство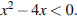

В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

1)

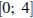
2)

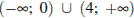
3)

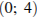
4)

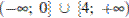
Ре­ше­ние.

х² - 4х = 0

х(х - 4) = 0

х = 0 или х – 4 = 0

           х = 4

 Чтобы посчитать знаки подставляем любое число (например 1) в неравенство и вычисляем: 1-4= -3. Единица была в промежутке от 0 до 4, ставим в этом промежутке знак «-», в квадратичных неравенствах знаки чередуются =>в двух промежутках ставим знак «+». Получим:

-∞____+____˳_____-____˳____+______

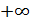
              0             4

Т.к. в неравенстве знак «<»,  => в ответ идут промежутки с минусами, точки проколоты, т.к. нет знака равно, =>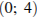

Ответ: 2)

4. Ре­ши­те не­ра­вен­ство .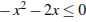

В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

1)

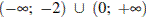
2)

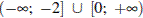
3)

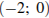
4)

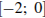
Ре­ше­ние.

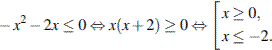
Про­из­ве­де­ние двух со­мно­жи­те­лей будет боль­ше нуля, если его со­мно­жи­те­ли имеют оди­на­ко­вый знак.

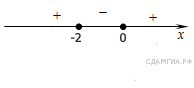
Пра­виль­ный ответ ука­зан под но­ме­ром 2

 5. Ре­ши­те не­ра­вен­ство .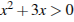

В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

1)

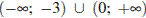
2)

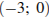
3)

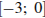
4)

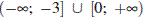
Ре­ше­ние.

Решим дан­ное не­ра­вен­ство:

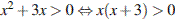. Про­из­ве­де­ние двух со­мно­жи­те­лей будет боль­ше нуля, если его со­мно­жи­те­ли имеют оди­на­ко­вый знак.

В дан­ном слу­чае это вы­пол­ня­ет­ся при сле­ду­ю­щих зна­че­ни­ях :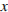

1) ;

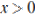2) ;

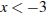Ре­ше­ни­ем не­ра­вен­ства будет яв­лять­ся объ­еди­не­ние этих про­ме­жут­ков: 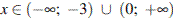, что со­от­вет­ству­ет пер­во­му ва­ри­ан­ту от­ве­та.

Ответ: 1

№ 6. Ре­ши­те не­ра­вен­ство .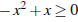

В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

1)

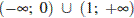
2)

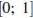
3)

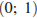
4)

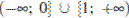
Ре­ше­ние.

Решим не­ра­вен­ство ме­то­дом ин­тер­ва­лов:

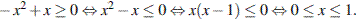Про­из­ве­де­ние равно нулю, если хотя бы один из его со­мно­жи­те­лей равен нулю.

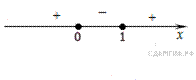
Пра­виль­ный ответ ука­зан под но­ме­ром 2.

 
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.