ДВИЖЕНИЯ АВТОТРАНСПОРТА

УДК 681.5

ВЫБОР РАЦИОНАЛЬНЫХ МАРШРУТОВ

ДВИЖЕНИЯ АВТОТРАНСПОРТА

В.Ф. Мацула, В.В. Фоминский

В статье рассматривается задача выбора рационального маршрута движения автотранспорта, предлагается специализированный алгоритм ее решения и реализующие его программные средства.

транспортная сеть, маршрут, автоматизация поиска маршрута, программное обеспечение

ЗАДАЧА ВЫБОРА РАЦИОНАЛЬНЫХ МАРШРУТОВ

Сегодня автомобильный транспорт – самая массовая отрасль. Масштабы грузоперевозок автомобильным транспортом огромны и связаны со всеми без исключения отраслями экономики. Затраты на грузоперевозки могут быть уменьшены за счет эффективного планирования передвижения автотранспорта. В настоящее время существует множество решений этой задачи. На их базе разработаны различные программные средства, однако они не всегда удовлетворяют потребностям конечного пользователя. Поэтому проблема автоматизации поиска рациональных маршрутов для конкретного предприятия является актуальной на сегодняшний день.

Маршрут - это путь следования транспорта при движении от начального до конечного пунктов с обязательным посещением некоторых промежуточных пунктов. Рациональный маршрут - это маршрут, наилучшим образом удовлетворяющий некоторому критерию (например, расстояние или время). Маршрутизация - это составление рациональных маршрутов движения.

Для нахождения удовлетворительного решения задачи маршрутизации с использование математических методов в качестве исходных данных необходима модель транспортной сети. Транспортная сеть – это совокупность дорог, пригодных для движения транспортных средств. Модель транспортной сети может быть представлена в виде графа, в котором вершины – это точки на сети, наиболее важные для определения расстояний или маршрутов движения, а дуги – отрезки транспортной сети, характеризующие наличие дорожной связи между соседними вершинами. Дуги графа характеризуются числами, которые могут иметь различный физический смысл. Чаще всего это расстояние, но может использоваться, например, время движения, количество потраченного топлива, суммарный показатель стоимости проезда и др.

Задача выбора рационального маршрута сводится к поиску на графе кратчайшего пути от некоторой начальной вершины до некоторой конечной вершины, при этом в маршрут могут входить некоторые обязательные промежуточные вершины. Под длиной кратчайшего пути при этом подразумевается сумма длин составляющих этот путь дуг. Частный случай – когда начальная и конечная вершины совпадают. Допускается прохождение любой промежуточной вершины несколько раз. Пример графа транспортной сети приведен на рис. 1.

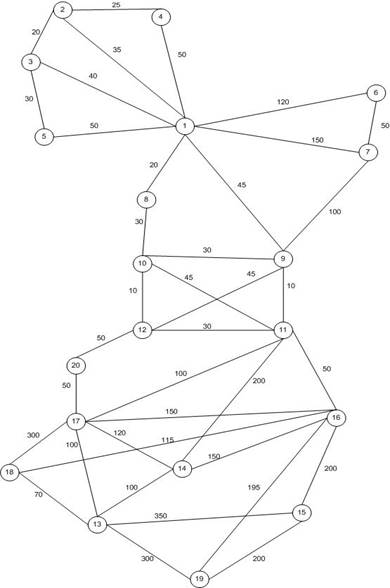
Рис. 1. Пример графа транспортной сети

Все специальные алгоритмы решения этой задачи являются итерационными, когда на каждой итерации наращивается или корректируется уже построенное к этому моменту множество кратчайших путей между вершинами графа. Недостатком этих алгоритмов является невозможность возвращения в одну из промежуточных точек, не предусматривается необходимость использования обязательных вершин. Как следствие, использование таких алгоритмов не всегда приводит к отысканию рационального маршрута.

Для поиска рациональных маршрутов предлагается специализированный алгоритм, основанный на методе сокращения графа за счет эквивалентных преобразований [1, с. 98-121]. На рис. 2 приведены примеры эквивалентных преобразований графа.

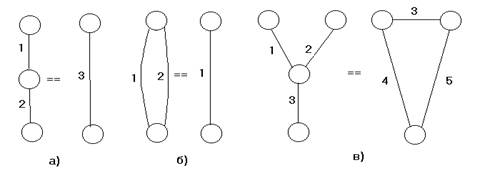
Рис. 2. Примеры эквивалентных преобразований графа:

а), в) – удаление необязательной вершины; б) – удаление параллельной дуги

Алгоритм предполагает решение задачи поиска в три этапа.

На первом этапе решения выполняется преобразование исходного графа маршрутной сети путем удаления необязательных вершин до тех пор, пока не останутся начальная, конечная и все обязательные вершины:

1.1) поиск необязательной вершины графа транспортной сети с минимальным числом входов и выходов;

1.2) удаление найденной вершины по правилам эквивалентных преобразований;

1.3) проверка образования в результате удаления вершины параллельного пути или петли. Если образовалась петля, то необходимо отбросить ее, как заведомо нерациональное решение. Если образовались параллельные пути, то необходимо выбрать путь с минимальной длиной;

1.4) если при удалении одной из параллельных дуг остается дуга, полученная в результате удаления вершины, то информация об удаленной вершине сохраняется в таблице истории удаления вершин;

1.5) шаги 1.1-1.4 повторяются до тех пор, пока не останутся только начальная, конечная и все обязательные вершины.

На рис. 3 приведен граф, полученный после первого этапа преобразований графа транспортной сети с рис. 1, когда вершина 3 является начальной, вершина 15 является конечной, обязательными являются вершины 8, 10,11.

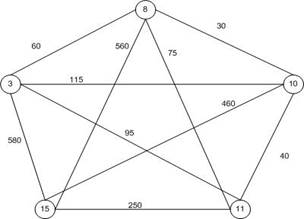
Рис. 3. Граф транспортной сети после первого этапа преобразований

Второй этап заключается в преобразовании полученного графа удаления вершин при сохранении всех параллельных путей до тех пор, пока не останутся только начальная и конечная вершины:

2.1) поиск обязательной вершины графа с минимальным числом входов и выходов;

2.2) удаление найденной вершины по правилам эквивалентных преобразований с сохранением информации об удаленной вершине в таблице истории удаления вершин;

2.3) проверка образования в результате замены вершины параллельного пути или петли. Если образовалась петля, то необходимо отбросить ее, как заведомо нерациональное решение. Дуги, образующие параллельные пути, не удаляются;

2.4) шаги 2.1-2.3 повторяются до тех пор, пока не останутся только начальная и конечная вершины.

На рис. 4 приведен граф, полученный после второго этапа преобразований графа транспортной сети с рис. 1.

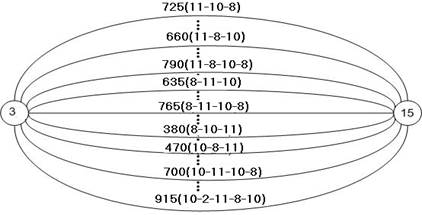
Рис.4. Граф транспортной сети после второго этапа преобразований

На третьем этапе среди дуг, соединяющих начальную и конечную вершины, ищется дуга с минимальной длиной, которая и будет соответствовать рациональному маршруту. Из истории удаления вершин для данной дуги можно узнать, через какие вершины проходит найденный маршрут. По графу на рис.4 видно, что рациональный маршрут для транспортной сети с рис. 1 соответствует дуге с длиной 380 и состоит из последовательности вершин 3-8-10-11-15.

АВТОМАТИЗАЦИЯ ВЫБОРА РАЦИОНАЛЬНОГО МАРШРУТА

Разработанная автоматизированная система поиска рациональных маршрутов ориентирована, главным образом, на автотранспортные предприятия, занимающиеся междугородними и международными грузовыми автоперевозками. Кроме того, данная система также может использоваться небольшими предприятиями для планирования маршрутов движения собственного транспорта в пределах населенного пункта.

Автоматизированная система поиска рациональных маршрутов обладает следующими возможностями:

l Ведение базы данных транспортных средств.

l Ведение базы данных транспортной сети.

l Решение задачи поиска рациональных маршрутов движения.

l Формирование и печать сведений по найденному маршруту движения.

l Формирование и печать сопровождающей рейс документации (путевые листы и т.п.), соответствующей найденному маршруту.

l Экспорт бухгалтерской документации в систему бухгалтерского учета.

l Получение справочной информации о расстояниях между смежными пунктами из базы транспортной сети.

Система поиска рациональных маршрутов реализована на базе среды разработки «1С: Предприятие» версии 7.7. Программная реализация выполнена на базовых объектах данной среды и поэтому может использоваться с любой компонентой «1С: Предприятие» версии 7.7. Система может применяться как самостоятельная конфигурация, так и в рамках функционального блока какой-либо другой конфигурации. Она открыта для внесения изменений для специалистов, программирующих на встроенном языке «1С:Предприятия 7.7».

Разработанная система установлена на компьютеры пользователей Калининградского транспортного предприятия ООО «Цепрусс-Импекс».

ВЫВОДЫ

Результаты эксплуатации системы показали, что ее использование позволяет повысить эффективность работы менеджеров-экспедиторов за счет сокращения времени на планирование маршрутов движения автотранспорта, улучшения и автоматизации документооборота. Система проста и удобна в эксплуатации за счет привычного интерфейса, является открытой для внесения изменений и дальнейшего развития. Получаемые в результате использования автоматизированной системы рациональные маршруты приводят к снижению затрат на перевозку грузов.

12 Следующая ⇒