
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема. Применение производной. Повторение
Тема. Применение производной. Повторение
Нахождение наибольшего и наименьшего значений функции
Алгоритм нахождения наибольшего и наименьшего значения функции на отрезке:
1) Найти f ‘(x).
2) Найти критические точки и отобрать те точки, которые лежат на отрезке [a:b] и вычислить значение функции в этих точках.
3) Найти значения функции на концах промежутка.
4) Сравнить полученные значения. Выбрать из них наибольшее и наименьшее, которые будут соответствовать большим и наименьшим значениям функции f.
Пример. Найти наибольшее и наименьшее значения функции у = 2х2-8х+6 на [-1;4].
Решение: у'= 4х-8
4х – 8=0
4х = 8
х = 2
2ϵ[-1;4]
f(-1)=2+8+6=16
f(2)=8-16+6=-2
f(4)=32-32+6=6
Ответ: min f(x) = -2; min f(x) = 16.
[-1;4] [-1;4]
ЗАДАНИЕ к уроку. Для закрепления материала решить задания.
В классной работе самостоятельно выполнить следующие задания:
1. Найдите угол наклона касательной к графику функции f(x)= 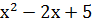 в точке х=1.
в точке х=1.
2. Найти промежутки монотонности и экстремумы функции:
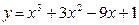
3. Найти наибольшее и наименьшее значения функции:
а) 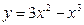 на [0;1]
на [0;1]
4. Исследовать функцию и построить ее график:
а) 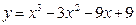
Задание на дом:
1. Найти промежутки монотонности и экстремумы функции:
а) 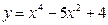
2. Исследовать функцию и построить ее график:
а) 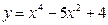
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|