ПОГРЕШНОСТИ ИЗМЕРЕНИЙ И СРЕДСТВ ИЗМЕРЕНИЙ

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Кузбасский государственный технический университет
имени Т. Ф. Горбачева»

Кафедра электроснабжения горных и промышленных предприятий

Р. В. Беляевский

ПОГРЕШНОСТИ ИЗМЕРЕНИЙ И СРЕДСТВ ИЗМЕРЕНИЙ

Рекомендовано для использования в учебном процессе
учебно-методической комиссией специальности

140211 «Электроснабжение» и направления

140400 «Электроэнергетика и электротехника»

Кемерово 2011

Рецензенты:

Ефременко В. М., заведующий кафедрой ЭГПП

Завьялов В. М., председатель УМК направления

140400 «Электроэнергетика и электротехника»

Беляевский Роман Владимирович.Погрешности измерений и средств измерений [Электронный ресурс] : метод. указания к практическим занятиям по дисциплине «Метрология, стандартизация и сертификация» для студентов специальности 140211 «Электроснабжение» и направления 140400 «Электроэнергетика и электротехника», профиль «Электроснабжение» всех форм обучения / Р. В. Беляевский. – Электрон. дан. – Кемерово : КузГТУ, 2011. – 1 электрон. опт. диск (CD-ROM) ; зв. ; цв. ; 12 см. – Систем. требования : Pentium IV ; ОЗУ 32 Мб ; Windows ХР ; (CD-ROM-дисковод) ; мышь. – Загл. с экрана.

Приведена классификация погрешностей измерений
и средств измерений, а также основные принципы описания
и оценивания погрешностей. Рассмотрены общие подходы к обнаружению и исключению систематических погрешностей и вероятностному описанию случайных погрешностей. Приведены примеры решения типовых задач и задачи для самостоятельного решения по теме «Погрешности измерений и средств измерений».

1. ЦЕЛЬ РАБОТЫ

1. Ознакомиться с классификацией погрешностей измерений и средств измерений.

2. Изучить основные принципы описания и оценивания погрешностей, а также общие подходы к обнаружению и исключению систематических погрешностей и вероятностному описанию случайных погрешностей.

3. Ознакомиться с примерами решения типовых задач
и закрепить теоретические знания, полученные в ходе практической работы, на основе задач для самостоятельного решения.

2. ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

2.1. Классификация погрешностей измерений и средств
измерений

Применяемые при измерениях методы и средства измерений не являются идеальными, а органы восприятия экспериментатора (оператора) не могут идеально воспринимать показания приборов. Поэтому после завершения процесса измерения всегда остается некоторая неопределенность в информации об объекте измерения, т. е. получить истинное значение физической величины невозможно. Однако, это понятие введено в теорию измерений, при этом различают истинное и действительное значения измеряемой величины и результат измерения.

Истинное значение физической величины –это значение физической величины, которое идеальным образом характеризует
в количественном и качественном отношении соответствующую физическую величину. Действительное значение физической величины – значение физической величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него. Результат измерения – значение физической величины, полученное путем ее измерения. Результат измерения представляет собой приближенную оценку истинного значения физической величины.

Остаточная неопределенность в информации об объекте измерения может характеризоваться различными мерами неопределенности. В метрологии мерой неопределенности результата измерений является погрешность результата измерения.

Под погрешностью результата измерения (погрешностью измерения)понимается отклонение результата измерения X от истинного (действительного) значения Q измеряемой величины:

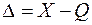. (1)

Погрешность измерения указывает границы неопределенности значения измеряемой величины. Истинное значение физической величины применяется при решении теоретических задач метрологии. На практике пользуются действительным значением. За действительное значение физической величины при однократных измерениях, как правило, принимают значение, полученное
с помощью эталонного средства измерений, а при многократных измерениях – среднее арифметическое ряда отдельных измерений, входящих в данный ряд. В зависимости от решаемой задачи могут использоваться и другие значения.

Погрешностью средства измерений называется разность между показанием средства измерений и истинным (действительным) значением измеряемой величины.

По способу выражения различают абсолютную, относительную и приведенную погрешности.

Абсолютная погрешность – это погрешность, выраженная
в единицах измеряемой величины и определяемая согласно выражению (1). Абсолютная погрешность сама по себе не может служить показателем точности измерений, поэтому вводится понятие относительной погрешности.

Относительная погрешность – это погрешность, выраженная отношением абсолютной погрешности к действительному значению измеряемой величины. Она является более наглядной характеристикой оценки качества результата измерения по сравнению с абсолютной погрешностью. Относительная погрешность выражается в относительных единицах (в процентах) и определяется по выражению:

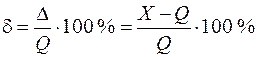. (2)

Приведенная погрешность – это относительная погрешность, в которой абсолютная погрешность средства измерений отнесена к условно принятому значению Q_N,постоянному
на всем диапазоне измерений или его части:

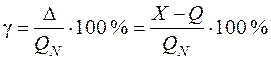. (3)

Условно принятое значение величины Q_N называют нормирующим значением. За нормирующее значение, как правило, принимают верхний предел измерений (максимальное значение измеряемой величины), т. е. Q_N = Q_max. Указание погрешности измерений в виде приведенной относительной погрешности свидетельствует о том, что абсолютная погрешность измерений Δ постоянна на всем диапазоне измерений.

Проанализировав формулы (2) и (3), можно построить графики зависимости относительных погрешностей δ и γ от показания измерительного прибора с односторонней шкалой (рис. 1). Поделив шкалу прибора на четыре равные части от нуля до Q_max, получим, что относительная погрешность δ максимальна в 1-й четверти шкалы и минимальна в 4-й четверти шкалы.

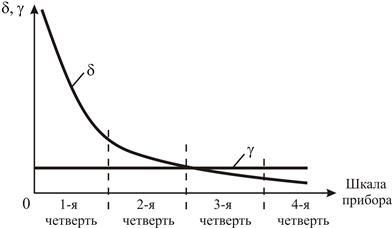
Рис. 1. Графики зависимости относительной и приведенной
погрешностей от показания измерительного прибора

На основании анализа полученных графиков зависимости можно сделать следующие выводы.

1. Для получения наименьшей относительной погрешности δ необходимо использовать 4-ю или 3-ю четверть шкалы прибора.

2. Из графика зависимости γ = f(Q)следует, что приведенная относительная погрешность не зависит от показания прибора. Поэтому приведенная погрешность γ положена в основу класса точности электромеханических приборов. В соответствии с ГОСТ 8.401–80 электромеханические приборы поделены на девять классов точности (табл. 1).

Таблица 1

Классы точности электромеханических приборов

Класс точности	1-й	2-й	3-й	4-й	5-й	6-й	7-й	8-й	9-й
γ, %	0,02	0,05	0,1	0,2	0,5	1,0	1,5	2,5	4,0

Если в формулу (2) подставить абсолютную погрешность, выраженную через формулу (3), то получим формулу, связывающую относительную и приведенную погрешности:

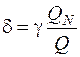. (4)

Относительная погрешность косвенных измерений определяется по формуле:

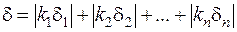, (5)

где k₁, k₂, …, k_n – показатели степени степенного многочлена;
δ₁, δ₂, …, δ_n – относительные погрешности прямых измерений.

Относительная и приведенная погрешности могут быть как положительными, так и отрицательными. На практике формула (5) чаще всего ограничивается двумя слагаемыми.

По характеру проявления различают систематическую и случайную погрешности, а также грубые погрешности (промахи).

Систематическая погрешность –составляющая погрешности результата измерения, остающаяся постоянной для данного ряда измерений или же закономерно изменяющаяся при повторных измерениях физической величины постоянного размера.

Случайная погрешность –составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) в серии повторных измерений физической величины постоянного размера, проведенных с одинаковой тщательностью в одинаковых условиях. В появлении таких погрешностей нет какой-либо закономерности, они проявляются при повторных наблюдениях в виде некоторого разброса полученных результатов.

Грубые погрешности (промахи) –это такие погрешности, которые при исправных средствах измерений и корректных действиях экспериментатора (оператора) не должны появляться. Проявляются они в том, что результаты отдельных измерений резко отличаются от остальных.

Особое место среди погрешностей занимают прогрессирующие (дрейфовые) погрешности. Их особенностью является то, что они могут быть скорректированы и учтены только в данный момент времени, а в дальнейшем вновь непредсказуемо изменяются. Прогрессирующая погрешность является понятием, которое не может быть сведено к понятиям случайной и систематической погрешностей, однако в нормативных документах ее определяют как один из видов систематической погрешности.

В зависимости от источника возникновения различают методическую, инструментальную и субъективную погрешности.

Субъективные погрешности связаны с индивидуальными особенностями оператора. Разновидностями субъективных погрешностей являются погрешности отсчитывания, интерполяции и параллакса. Погрешность отсчитывания возникает из-за ошибок в отсчете показаний (примерно 0,1 деления шкалы). Погрешность интерполяции – это погрешность, вызванная неточностью нахождения промежуточного значения какой-либо изменяющейся величины по ряду соседних известных значений. Погрешностью параллакса называется погрешность, обусловленная изменением видимого положения стрелки прибора относительно удаленного фона в зависимости от положения оператора. В основном же, систематические погрешности возникают из-за методической и инструментальной составляющих.

Методическая составляющая погрешности обусловлена метода измерения, приемами использования средства измерений, некорректностью расчетных формул и округления результатов измерений.

Инструментальная составляющая погрешности возникает из-за собственной погрешности средства измерений, определяемой классом точности, влиянием средства измерений на результат измерения и ограниченной разрешающей способности средства измерений.

По условиям возникновения у средств измерений различают основную и дополнительные погрешности. Каждое средство измерений предназначено для работы в определенных условиях, указываемых в нормативно-технической документации. При этом отдельно указывают нормальные условия применения средств измерений, т. е. условия, при которых величины, влияющие на погрешности данного средства измерений, находятся в пределах нормальной области значений, и рабочие условия применения – условия работы, при которых значения влияющих величин выходят за пределы нормальных, но находятся в пределах рабочих областей. Погрешность средства измерений, определенная
при нормальных условиях, называется основной. Погрешность, обусловленная выходом значений влияющих величин за пределы нормальных значений, называется дополнительной. Для оценивания дополнительных погрешностей в документации на средство измерений обычно указывают нормы изменения показаний
при выходе условий измерения за пределы нормальных.

По характеру поведения измеряемой величины в процессе измерения выделяют статические и динамические погрешности.

Статическая погрешность проявляется при работе средства измерений в статическом режиме, когда показания средства измерений не зависят от его динамических свойств, или когда этой зависимостью можно пренебречь.

Динамическая погрешность возникает при работе средства измерений в динамическом режиме и определяется двумя факторами: динамическими (инерционными) свойствами средства измерений и характером изменения измеряемой величины.

У средств измерений часто можно выделить составляющие погрешности, не зависящие от значения измеряемой величины,
и погрешности, изменяющиеся пропорционально измеряемой величине. Такие составляющие называются, соответственно, аддитивными и мультипликативными погрешностями.

Классификация погрешностей измерений и средств измерений приведена в табл. 2.

Таблица 2

Классификация погрешностей измерений и средств измерений

Классификационный признак	Виды погрешностей
Классификационный признак	измерений	средств измерений

Способ выражения	Абсолютная Относительная	Абсолютная Относительная Приведенная
Характер проявления	Систематическая Случайная Грубая	Систематическая Случайная
Условия возникновения: нормальные рабочие	– –	Основная Дополнительная
Источник возникновения	Методическая Инструментальная Субъективные	– Несовершенство средств измерений Отсчитывания Интерполяции Параллакса
Характер поведения измеряемой величины	–	Статическая Динамическая
По характеру зависимости от измеряемой величины		Аддитивные Мультипликативные

2.2. Принципы описания и оценивания погрешностей

В основе современных подходов к оцениванию погрешностей лежат принципы, обеспечивающие выполнение требований единства измерений.

Для целей исследования и оценивания погрешности описываются с помощью определенных математических моделей (систематическая, случайная, методическая, инструментальная и др.). Для выбранной модели определяются характеристики, пригодные для количественного выражения тех или иных ее свойств. Задачей обработки данных при измерениях и является нахождение оценок этих характеристик. Характеристики погрешности (показатели точности) оцениваются приближенно. Точность оценок согласовывается с целью измерения.

Выбор модели погрешности обусловлен сведениями об ее источниках, как априорными, так и полученными в ходе измерительного эксперимента. Модели разделяют на детерминистские
и недетерминистские (случайные). Для систематических погрешностей справедливы детерминистские модели, при которых систематическая погрешность по определению может быть представлена постоянной величиной, либо известной зависимостью (линейная, периодическая и др.). Общей моделью случайной погрешности служит случайная величина, обладающая функцией распределения вероятностей.

Характеристики случайной погрешности делятся на точечные и интервальные. Для описания погрешностей результата измерения чаще всего используют интервальные оценки. Это означает, что границы, в которых может находиться погрешность, находят как отвечающие некоторой вероятности. Однако, в некоторых случаях, когда нет возможности или необходимости оценить границы погрешности (например, неизвестна функция распределения вероятностей погрешности), используют точечные характеристики. Точечными характеристиками являются среднее квадратическое отклонение случайной погрешности, дисперсия и др.

В целях единообразия представления результатов и погрешностей измерений показатели точности и формы представления результатов измерений стандартизованы.

Распространенной ошибкой при оценивании результатов
и погрешностей измерений является вычисление их и запись
с чрезмерно большим числом значащих цифр. Этому способствует использование для расчетов средств вычислительной техники. Необходимо помнить, что поскольку погрешности измерений указывают лишь неопределенность результатов, т. е. дают представление о том, какие цифры в числовом значении результата являются сомнительными, то их не требуется знать очень точно. Для технических измерений допустимой считается неточность оценивания погрешности в 15–20 %.

Стандартом установлено, что в численных показателях точности измерений (в том числе и в погрешности) должно быть
не более двух значащих цифр. При записи результатов измерений наименьшие разряды числовых значений результата измерения
и численных показателей точности должны быть одинаковы.

Практикой выработаны следующие правила округления результатов и погрешностей измерений.

1. Лишние цифры в целых числах заменяются нулями,
а в десятичных дробях отбрасываются. Если десятичная дробь
в числовом значении результата измерения оканчивается нулями, то нули отбрасываются только до того разряда, который соответствует разряду погрешности. Например, если результат измерения 2,0700, погрешность 0,001, то результат округляют до 2,070.

2. Если цифра старшего из отбрасываемых разрядов меньше 5, то остающиеся цифры числа не изменяют. Например, число 235435 при сохранении четырех значащих цифр должно быть округлено до 235400, число 235,435 – до 235,4.

3. Если цифра старшего из отбрасываемых разрядов больше или равна 5, но за ней следуют отличные от нуля цифры, то последнюю оставляемую цифру увеличивают на единицу. Например, при сохранении трех значащих цифр число 18598 округляют до 18600, число 152,56 – до 153.

4. Если отбрасываемая цифра равна 5, а следующие за ней цифры неизвестны или нули, то последнюю сохраняемую цифру не изменяют, если она четная и увеличивают, если она нечетная. Например, число 22,5 при сохранении двух значащих цифр округляют до 22, а число 23,5 – до 24.

2.3. Обнаружение и исключение систематических погрешностей

Источниками систематических составляющих погрешности измерения могут быть все его компоненты: метод измерения, средства измерений и оператор. Оценивание систематических составляющих погрешности представляет достаточно трудную метрологическую задачу. Важность ее определяется тем, что знание систематической погрешности позволяет внести соответствующую поправку в результат измерения и тем самым повысить его точность. Трудность же заключается в сложности обнаружения систематической погрешности, поскольку она не может быть выявлена путем повторных измерений (наблюдений). Таким образом, проблема обнаружения систематических погрешностей является едва ли не главной в борьбе с ними.

Постоянные инструментальные систематические погрешности обычно выявляют посредством поверки средства измерений. Поверкойназывается определение метрологическим органом погрешностей средства измерений и установление пригодности средства измерений к применению. Поверка производится путем сравнения показаний поверяемого прибора с показаниями более точного (эталонного) средства измерений. Если на поверяемой отметке шкалы показания поверяемого прибора равны Q, а эталонного X, то погрешность поверяемого прибора на этой отметке:

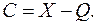(6)

Поверка средств измерений производится в соответствии
с требованиями, устанавливаемыми в нормативно-технической документации, а ее результаты указываются в свидетельстве
о поверке или в паспорте прибора. Обнаруженные таким образом систематические погрешности исключаются из результата измерения путем введения поправки. Поправка – это значение величины, вводимое в неисправленный результат измерения с целью исключения составляющих систематической погрешности. Из формулы (6) следует, что истинное значение величины Qравно:

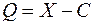т. е. поправка (–C) представляет собой погрешность, взятую
с противоположным знаком.

Для обнаружения изменяющейся систематической погрешности рекомендуется построить график, на котором нанесены результаты измерений в той последовательности, в какой они были получены. Общий вид расположения полученных точек позволяет обнаружить наличие закономерного изменения результатов измерений и сделать вывод о присутствии в них систематической погрешности. Простейшим, но часто встречающимся случаем погрешности, изменяющейся по определенному закону, является погрешность, прогрессирующая по линейному закону, например, пропорционально времени.

Систематические составляющие, обусловленные несовершенством методов измерений, ограниченной точностью расчетных формул, положенных в основу измерений, влиянием средств измерений на объект, свойства которого измеряются, относятся
к методическим погрешностям. Единых рекомендаций по обнаружению и оцениванию методических составляющих систематической погрешности нет. Поэтому, задача решается в каждом конкретном случае индивидуально, на основе анализа применяемого метода измерений, результаты которого часто зависят
от квалификации и опыта оператора.

Полученная при этом оценка систематической погрешности, в свою очередь, имеет некоторую погрешность из-за погрешностей в определении измеряемой величины,а также из-за наличия инструментальной погрешности средства измерений. Эта погрешность при введении поправки не исключается и называется неисключенным остатком систематической погрешности(неисключенной систематической погрешностью).

Субъективные систематические погрешности связаны с индивидуальными особенностями оператора. При проектировании современных средств измерений принимаются меры к тому, чтобы максимально исключить возможность появления субъективных погрешностей. По этой причине принято считать субъективные погрешности пренебрежимо малыми и при анализе погрешностей не принимать их в расчет. Вместе с тем неточные действия оператора могут привести к запаздыванию или опережению фиксации моментов времени при отсчете показаний, неточности отсчитывания значений измеряемой величины по шкале стрелочного прибора из-за параллакса и др. Поэтому для того чтобы избежать субъективных погрешностей, необходимо точно соблюдать правила эксплуатации средств измерений и иметь навыки работы с измерительной техникой.

В практике измерений применяется несколько методов, позволяющих за счет некоторого усложнения процедуры измерений получить результат измерения свободным от систематической погрешности. К ним относятся метод замещения, метод противопоставления и метод компенсации погрешности по знаку.

Метод замещения дает наиболее полное решение задачи компенсации постоянной систематической погрешности и представляет собой разновидность метода сравнения. Сравнение производится путем замены измеряемой величины известной величиной и таким образом, чтобы воздействием известной величины привести средство измерений в то состояние, которое оно имело при воздействии измеряемой величины.

Метод противопоставления заключается в том, что измерения проводят два раза, причем так, чтобы величина, вызывающая погрешность при первом измерении, оказала противоположное действие на результат второго измерения.

Метод компенсации погрешности по знаку также предусматривает проведение измерения в два этапа, выполняемых так, чтобы постоянная систематическая погрешность входила в показания средства измерений на каждом этапе с разными знаками.
За результат измерения принимают полусумму показаний – систематические погрешности при этом взаимно компенсируются.

2.4. Случайные погрешности и их вероятностное описание

Когда при проведении в одинаковых условиях повторных измерений одной и той же величины получают результаты, отличающиеся друг от друга, это свидетельствует о наличии в них случайных погрешностей. Каждая такая погрешность возникает вследствие одновременного воздействия на результат измерения случайных возмущений и сама является случайной величиной.
В этом случае предсказать результат отдельного измерения и исправить его введением поправки невозможно. Можно лишь с определенной долей уверенности утверждать, что истинное значение измеряемой величины находится в пределах разброса результатов измерений от Q_min до Q_m_ах. Однако остается неясным, какова вероятность появления того или иного значения погрешности, какое из множества лежащих в этой области значений величины принять за результат измерения и какими показателями охарактеризовать случайную погрешность результата измерения. Для этого требуется принципиально иной подход, чем при анализе систематических погрешностей. Данный подход основывается
на рассмотрении результатов измерений и случайных погрешностей как случайных величин. Методы теории вероятностей и математической статистики позволяют установить статистические закономерности появления случайных погрешностей и на основании этих закономерностей дать количественные оценки результата измерения и его случайной погрешности.

Для характеристики свойств случайной величины в теории вероятностей используют понятие закона распределения вероятностей случайной величины. Различают две формы описания закона распределения: интегральную и дифференциальную. В метрологии преимущественно используется дифференциальная форма – закон распределения плотности вероятностей случайной величины. Закон распределения дает полную информацию о свойствах случайной величины и позволяет оценнить результат измерения и его случайную погрешность.

Для описания частных свойств случайных величин используются их числовые характеристики. Из числовых характеристик наибольший интерес представляют математическое ожидание
и дисперсия случайной величины. Дисперсия характеризует рассеяние отдельных значений случайной величины относительно среднего значения и имеет размерность квадрата случайной величины. Однако на практике чаще всего пользуются положительным квадратным корнем из дисперсии – средним квадратическим отклонением (СКО), которое имеет размерность самой случайной величины.

Задача оценки результата измерения состоит в том, чтобы по полученным экспериментальным путем данным, содержащим случайные погрешности, найти оценку истинного значения измеряемой величины. При этом полагают, что систематические погрешности в результате измерения отсутствуют или исключены.

К оценкам, получаемым по статистическим данным, предъявляются требования состоятельности, несмещенности и эффективности. Оценка называется состоятельной,если при увеличении числа наблюдений она стремится к истинному значению оцениваемой величины.

Оценка называется несмещенной,если ее математическое ожидание равно истинному значению оцениваемой величины.
В том случае, когда можно найти несколько несмещенных оценок, то лучшей из них считается та, которая имеет наименьшую дисперсию. Чем меньше дисперсия оценки, тем более эффективнойсчитают эту оценку.

Способы нахождения оценок результата измерения зависят от вида функции распределения и от имеющихся соглашений
по этому вопросу, регламентируемых в рамках законодательной метрологии. На практике встречаются различные формы кривой закона распределения, однако чаще всего имеют дело с нормальным и равномерным распределением плотности вероятностей.

Для количественной оценки случайных погрешностей и установления границ случайной погрешности результата измерения могут использоваться: предельная погрешность, интервальные оценки, числовые характеристики закона распределения. Выбор конкретной оценки определяется необходимой полнотой сведений о погрешности, назначением измерений и характером использования их результатов. Комплексы оценок показателей точности установлены стандартами.

Наиболее универсальными и информативными являются интервальные оценки. Площадь, заключенная под кривой плотности распределения погрешностей, отражает вероятность всех возможных значений погрешности и по условиям нормирования равна единице. Эту площадь можно разделить вертикальными линиями на несколько частей. Абсциссы таких линий называются квантилями. Так, на рис. 2 абсцисса ΔQ₁ есть 25 %-я квантиль,
т. к. площадь под кривой f(ΔQ) слева от нее составляет 25 % всей площади, а абсцисса ΔQ₂соответствует 75 %-й квантили. Между ΔQ₁и ΔQ₂заключено 50 % всех возможных значений погрешности, а остальные лежат вне этого интервала.

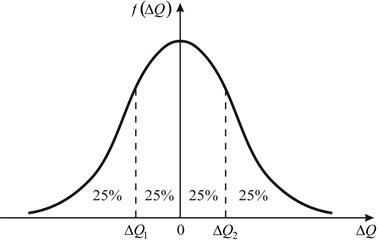
Рис. 2. Квантильные оценки случайной величины

Квантильная оценка погрешности представляется интервалом от –ΔQ(Р) до +ΔQ(Р), на котором с заданной вероятностью Рвстречаются Р∙100 % всех возможных значений случайной погрешности. Интервал с границами ±ΔQ(Р) называется доверительным интервалом случайной погрешности, а соответствующая ему вероятность – доверительной вероятностью.Принято границы доверительного интервала (доверительные границы) указывать симметричными относительно результата измерения.

Так как квантили, ограничивающие доверительный интервал погрешности могут быть выбраны различными, то при оценивании случайной погрешности доверительными границами необходимо одновременно указывать значение принятой доверительной вероятности (например, ±0,3 ед. при Р = 0,95).

Доверительные границы случайной погрешности ΔQ(Р), соответствующие доверительной вероятности Р,определяются
по формуле:

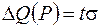, (7)

где t – коэффициент, зависящий от доверительной вероятности Ри формы закона распределения; σ – среднее квадратическое отклонение.

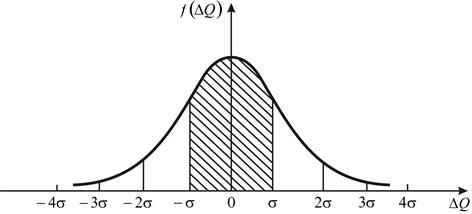
Рис. 3. К понятию доверительных интервалов

На графике нормального распределения погрешностей
(рис. 3) по оси абсцисс отложены интервалы с границами ±σ, ±2σ, ±3σ, ±4σ. Доверительные вероятности для этих интервалов приведены в табл. 3.

Таблица 3

Доверительные интервалы и доверительные вероятности

tσ	Р
±σ	0,68
±2σ	0,95
±3σ	0,997
±4σ	0,999

Как следует из табл. 3, оценка случайной погрешности группы измерений интервалом ±σ соответствует доверительной вероятности Р = 0,68. Такая оценка не дает уверенности в высоком качестве измерений, поскольку 32 % от всего числа измерений может выйти за пределы указанного интервала, что неприемлемо при однократных измерениях и дезинформирует оператора. Доверительному интервалу ±3σ соответствует Р =0,997. Это означает, что практически с вероятностью очень близкой к единице ни одно из возможных значений погрешности при нормальном законе ее распределения не выйдет за границы интервала. Поэтому, при нормальном распределении погрешностей, принято считать случайную погрешность с границами ±3σ предельной (максимально возможной) погрешностью. Погрешности, выходящие за эти границы, классифицируют как грубые или промахи.

В целях единообразия в оценивании случайных погрешностей интервальными оценками при технических измерениях доверительная вероятность принимается равной 0,95. Лишь для особо точных и ответственных измерений допускается применять более высокую доверительную вероятность.

3. ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

Задача 1.Измерено два значения напряжения (50 и 400 В) вольтметром с номинальным значением 400 В с одной и той же абсолютной погрешность 0,5 В. Какое напряжение будет измерено с меньшей погрешностью?

При решении задач по определению погрешности измерений необходимо правильно обозначить исходные данные. Так, напряжение измеряется рабочим вольтметром и обозначается
U₁ = 50 В, U₂ = 400 В, с одинаковой абсолютной погрешностью Δ₁= Δ₂ = 0,5 В. О виде шкалы вольтметра ничего не говорится, значит используется вольтметр с односторонней шкалой, у которого U_min= 0 и U_m_ах = 400 В, поэтому U_ном= 400 В.

Погрешность измерения определяем по формуле (2):

;

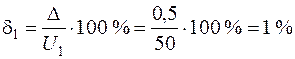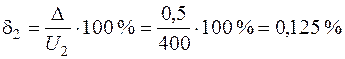Ответ: с меньшей погрешностью будет измерено напряжение 400 В.

Задача 2.В результате калибровки вольтметра магнитоэлектрической системы со шкалой 0…50 В и шагом шкалы 10 В получены показания образцового вольтметра (табл. 4).

Таблица 4

Исходные данные для задачи 2

U, В
U_изм, В	0,2	10,2	19,9	30,3	39,5	50,9

Определить приведенную относительную погрешность и назначить вольтметру класс точности.

Для определения приведенной погрешности γ необходимо воспользоваться формулой (3):

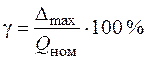Находим максимальную абсолютную погрешность Δ_m_ах=
= |50,9 – 50| = 0,9 В и номинальное значение U_ном =50– 0 = 50 В. Тогда

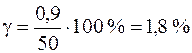Полученная приведенная погрешность γ находится между
7-м (1,5 %) и 8-м (2,5 %) классом точности по ГОСТ 8.401–80, поэтому назначаем вольтметру ближайший больший класс точности – 8-й .

Ответ: γ = 1,8 %; назначаем вольтметру 8-й класс точности.

Задача 3.Необходимо измерить напряжение 20 В многопредельным вольтметром 5-го класса точности (0,5 %) с пределами измерения 7,5 – 15 – 30 – 60 В, выбрать оптимальный предел измерения вольтметра и оценить относительную погрешность в выбранном пределе измерения.

При выборе предела измерения целесообразно представить положение стрелки вольтметра в каждом из четырех пределов при измерении заданного параметра (рис. 4).

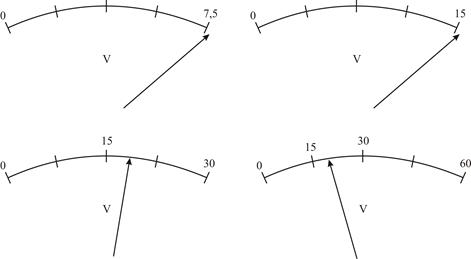
Рис. 4. Пояснение к задаче 3

Из рис. 4 следует, что при выборе пределов измерения 7,5 В или 15 В вольтметр будет зашкаливать. Пр