
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ЛИНЕЙНЫЕ ОБРАЗЫ В R3. Понятие алгебраической поверхности.. а. Плоскость.
ЛИНЕЙНЫЕ ОБРАЗЫ В R3
4. Понятие алгебраической поверхности.
Определение.Алгебраической поверхностью называется множество, которое в какой-нибудь декартовой системе координат может быть задано уравнением вида:
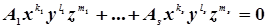
где все показатели степени – целые неотрицательные числа. Наибольшая из сумм: 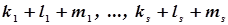 называется степенью уравнения, а также периодом алгебраической поверхности. Это определение означает, в частности, что сфера является алгебраической поверхностью второго порядка.
называется степенью уравнения, а также периодом алгебраической поверхности. Это определение означает, в частности, что сфера является алгебраической поверхностью второго порядка.
Перейдем к рассмотрению конкретных линейных образов в пространстве R3.
4.а. Плоскость.
1.  Уравнение плоскости
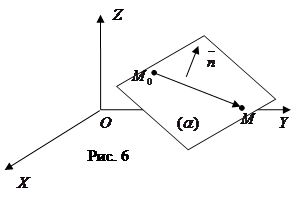
Уравнение плоскости  , проходящей через данную точку
, проходящей через данную точку 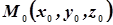 , перпендикулярно данному вектору
, перпендикулярно данному вектору 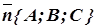 (рис. 6).
(рис. 6).
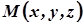 - текущая точка плоскости
- текущая точка плоскости  . Вектор
. Вектор 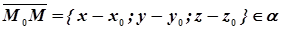 . Для любой точки плоскости векторы
. Для любой точки плоскости векторы 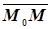 и
и 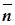 ортогональны, следовательно, их скалярное произведение равно
ортогональны, следовательно, их скалярное произведение равно 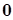 .
.
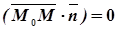 .
.
В уравнении перейдём к координатной форме:
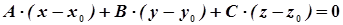 . (12)
. (12)
Уравнение (12) называется уравнением плоскости, проходящей через данную точку, перпендикулярно данному вектору.
2. Общее уравнение плоскости - это уравнение  степени с неизвестными
степени с неизвестными  , которое имеет вид:
, которое имеет вид:
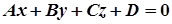 . (13)
. (13)
3. Уравнение плоскости, проходящей через три данные точки (рис. 7).
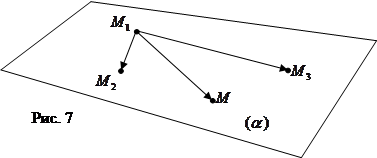 |
Пусть плоскости  принадлежат три точки
принадлежат три точки 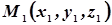 ,
, 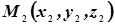 ,
, 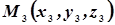 .
. 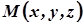 - текущая точка плоскости, тогда векторы
- текущая точка плоскости, тогда векторы 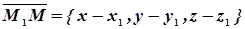 ,
, 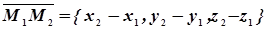 ,
, 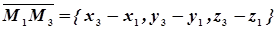 компланарны и, следовательно, смешанное произведение этих векторов равно нулю.
компланарны и, следовательно, смешанное произведение этих векторов равно нулю.
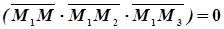 , или
, или 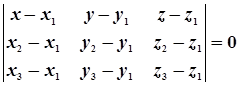 . (14)
. (14)
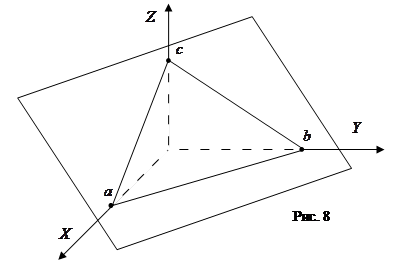 4. Уравнение плоскости «в отрезках»:
4. Уравнение плоскости «в отрезках»:
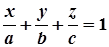 (15)
(15)
где а,b,с – величины отрезков, отсекаемых плоскостью от начала координат на осях координат (рис. 8).
5. Расстояние точки от плоскости.
Дана плоскость 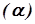 -
-  и точка
и точка 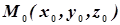 вне плоскости, тогда расстояние
вне плоскости, тогда расстояние 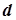 точки
точки 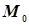 от плоскости
от плоскости 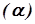 имеет вид:
имеет вид:
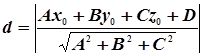 (16)
(16)
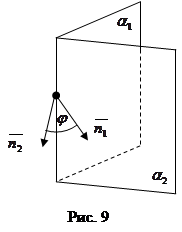 6. Угол между двумя плоскостями. Условие параллельности и перпендикулярности двух плоскостей (рис. 9).
6. Угол между двумя плоскостями. Условие параллельности и перпендикулярности двух плоскостей (рис. 9).
Даны две плоскости:
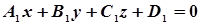 и
и
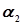
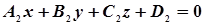
и 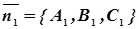 ;
; 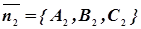 - нормальные векторы к соответствующим данным плоскостям.
- нормальные векторы к соответствующим данным плоскостям.
За угол между двумя плоскостями принимается угол между их нормальными векторами:
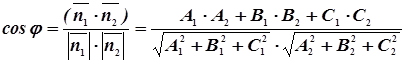 (17)
(17)
Если плоскости параллельны, то векторы 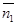 и
и 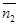 коллинеарны, и, следовательно,
коллинеарны, и, следовательно,
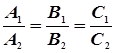 (18)
(18)
условие параллельности двух плоскостей.
Если плоскости перпендикулярны, то
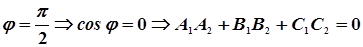 (19)
(19)
условие перпендикулярности двух плоскостей.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|