Тема занятия «Перпендикулярность прямой и плоскости»

Тема занятия «Перпендикулярность прямой и плоскости»

Определение. Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90 градусов. (Обозначается a⊥b)

Рассмотрим лемму о перпендикулярности двух параллельных прямых к третьей прямой.

Лемма.Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.

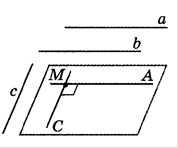
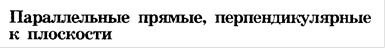
Определение.Прямая называется перпендикулярной к плоскости, если она перпендикулярная к любой прямой, лежащей в этой плоскости.

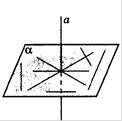
Теорема 1.Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.

Теорема 2.Если две прямые перпендикулярны к плоскости, то они параллельны.

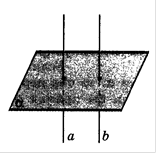
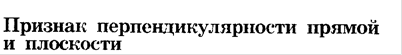
Теорема 3. (Признак перпендикулярности прямой и плоскости)

Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

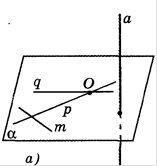
Теорема 4. ( О прямой, перпендикулярной к плоскости)

Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

Задача 2

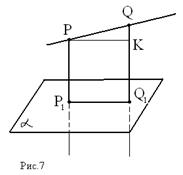
Через точки P и Q прямой РQ проведены прямые, перпендикулярные к плоскости α и пересекающие её соответственно в точках P₁ и Q₁. Найдите P₁Q₁, если PQ = 15 cм; PP₁ = 21,5 cм; QQ₁ = 33,5 cм.
Решение:

1) PP₁ ⊥ α и QQ₁ ⊥ α по условию ⇒ PP₁ ∥ QQ₁ (обосновать);
2) PP₁ и QQ₁ определяют некоторую плоскость β, α ⋂ β = P₁Q₁;
3) PP₁Q₁Q - трапеция с основаниями PP₁ и QQ₁, проведём PK ∥ P₁Q₁;
4) QK = 33,5 - 21,5 = 12 (см)

P₁Q₁ = PK =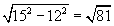

= 9 см.

Ответ: P₁Q₁ = 9 см.

№3

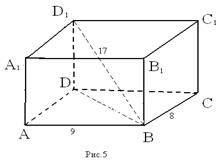
В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ АВ = 9 см; ВС = 8 см; ВD = 17 см. Найдите площадь BDD₁B₁.
Решение:

1) ∆ ABD: ∠BAD = 90°; АD = BC = 8 см;

ВD =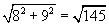

см;

2) ∆ DD₁B: ∠D₁DB = 90°;

DD₁ =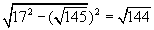

= 12 см;

3) S_BB_1D1D = BD ∙ DD₁ =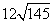

см².

Ответ: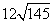

см².

№4

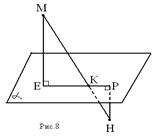
Отрезок МН пересекает плоскость α в точке К. Из концов отрезка проведены прямые МЕ и НР, перпендикулярные к плоскости α. НР = 4 см; МЕ = 12 см; НК = 5 см. Найдите отрезок РЕ.
Решение:

1) Т.к. прямые МЕ и НР перпендикулярны к плоскости α, то МЕ ∥ НР (обосновать) и через них проходит некоторая плоскость β. α ⋂ β = EP;
2)МЕ ⊥ EP; НР ⊥ EP(обосновать), т.е. ∠MEK = ∠HPK = 90°;

3) ∆ HPK: KP =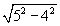

= 3 см;

4) ∠EMK = ∠PHK (накрест лежащие для параллельных прямых МЕ и НР и секущей МН),

тогда ∆ MEK ∆ HPK по двум углам и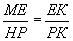

; т.е.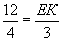

⇒ EK =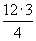

= 9 см,

РЕ = РК + КЕ, РЕ = 3 + 9 = 12 см.

Ответ: РЕ = 12 см.


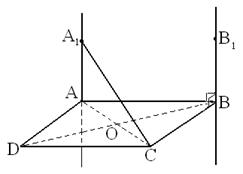
Через вершины А и В прямоугольника АВСD проведены параллельные прямые AA₁ и BB₁, не лежащие в плоскости прямоугольника. Известно, что AA₁ ⊥ AB, AA₁ ⊥ AD. Найдите B₁B, если B₁D = 25 см, AB = 12 см, AD = 16 см.	Через вершины А и В ромба АВСD проведены параллельные прямые AA₁ и BB₁, не лежащие в плоскости ромба. Известно, что BB₁ ⊥ BC,BB₁ ⊥ AB. Найдите A₁A, если A₁C = 13 см, BD = 16 см, AB = 10 см.
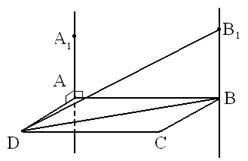
Решение:	Решение: .

Домашняя работа

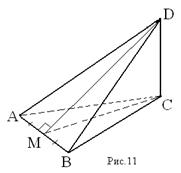
Дано: ∆ ABC; AB = AC = BC; CD ⊥ (ABC); AM = MB; DM = 15 дм; CD = 12 дм.
Найти: S_{∆ ADB}