Алгебра 10 кл. 6.05 – 8.05. Например

Алгебра 10 кл. 6.05 – 8.05

Дорогие дети! Теперь самое главное научиться решать однородные уравнения. У них свой метод решения.
Для этого:

1.важно понять, какие уравнения есть однородные

Уравнение называется однородным относительно sinх и cosх, если все его члены одной и той же степени относительно sinх и cosх ( угол может быть любым, но одинаковый и у синуса и косинуса) Степень функций может быть одинаково первой или второй или третьей и т.д. От этого уравнения бывают однородными первой степени, они имеют вид:

asin x +bcosx = 0;например: sin x +cosx = 0; 4sin 2x - 5cos2x = 0

однородные второй степени и они имеют вид:

asin ²x + bcosxsinx + c cos ²x = 0;например: 7sin ²x + 6cosxsinx + cos ²x = 0

2sin ²x - 5cosxsinx - 3 cos ²x = 0 ; sin ²3x + 4cos3xsin3x +9 cos ²3x = 0

a, b, c –коэффициенты. В правой части уравнения должен быть «0»!

Мы будем учиться решать однородные уравнения первой степени и второй степени

2. Чтобы решить однородное уравнение, надо:

а) перенести все его члены в левую часть;

б)получить однородное уравнение ;

в) разделить на cosх, если уравнение первой степени, на cos²х если уравнение второй степени;

г) решить полученное уравнение относительно tgх или выполнить замену и решить квадратное уравнение.

Например

1. sin x +cosx = 0

разделим на cosх, получим

tg x +1=0,

tg x =-1,

х= - π/4 + πk,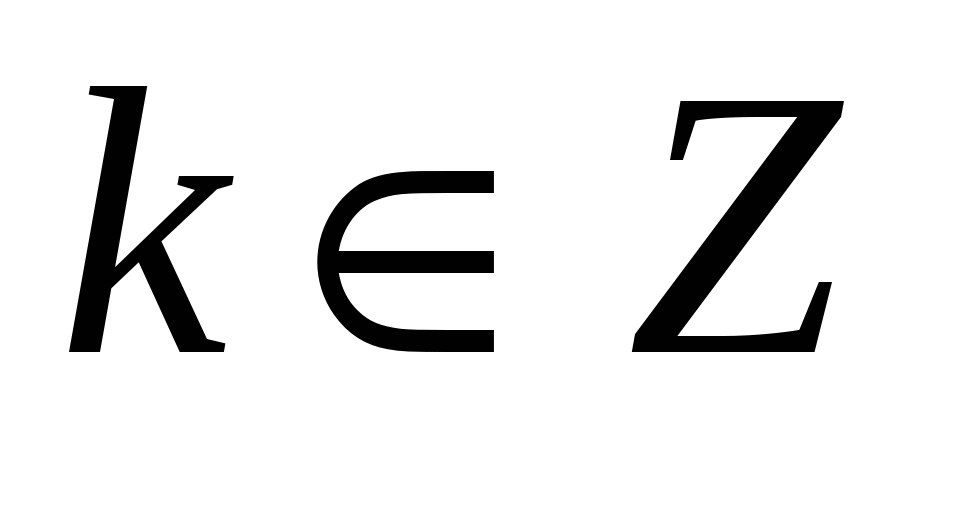

Ответ: - π/4 + πk,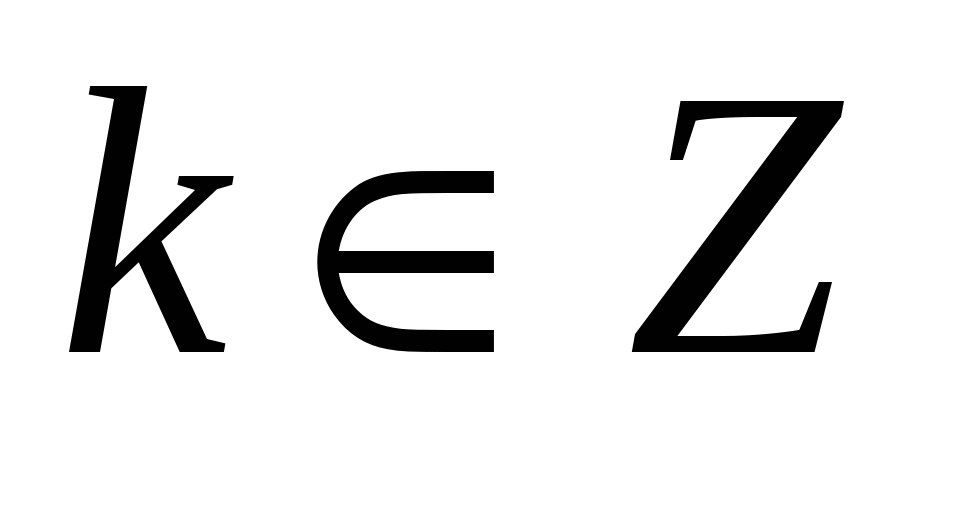

2. sin ² x + 4 sin x · cos x + 3 cos ² x = 0 ,

t g² x + 4 tg x + 3 = 0 , отсюда y ² + 4y +3 = 0 ,

корни этого уравнения: y₁ = -1, y₂ = -3, отсюда

1) tgx = –1, 2) tg x = –3,

х₁= - π/4 + πk, 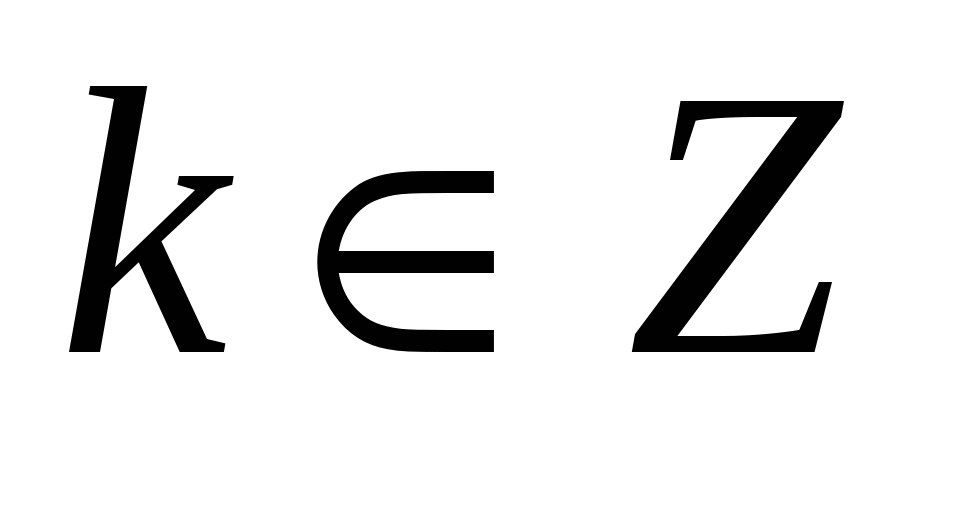; х₂= -arctg3 +πn,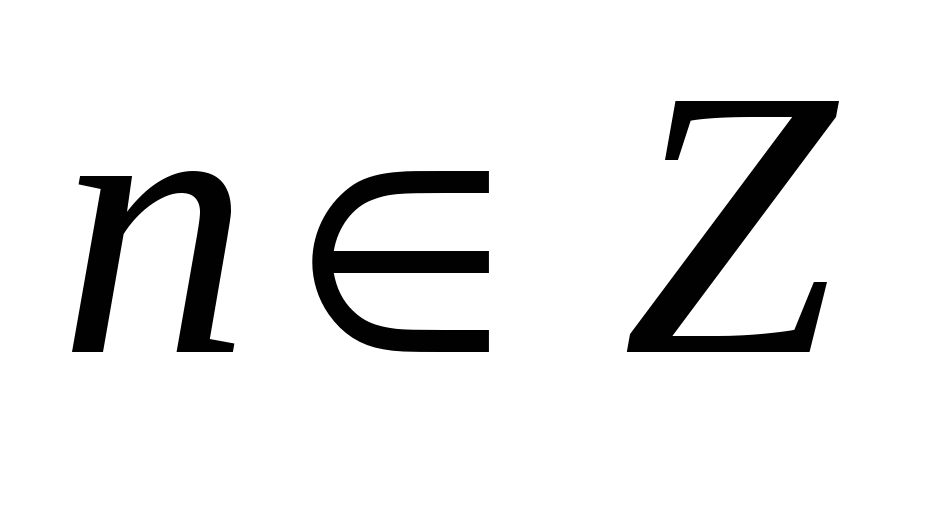

Ответ: - π/4 + πk, 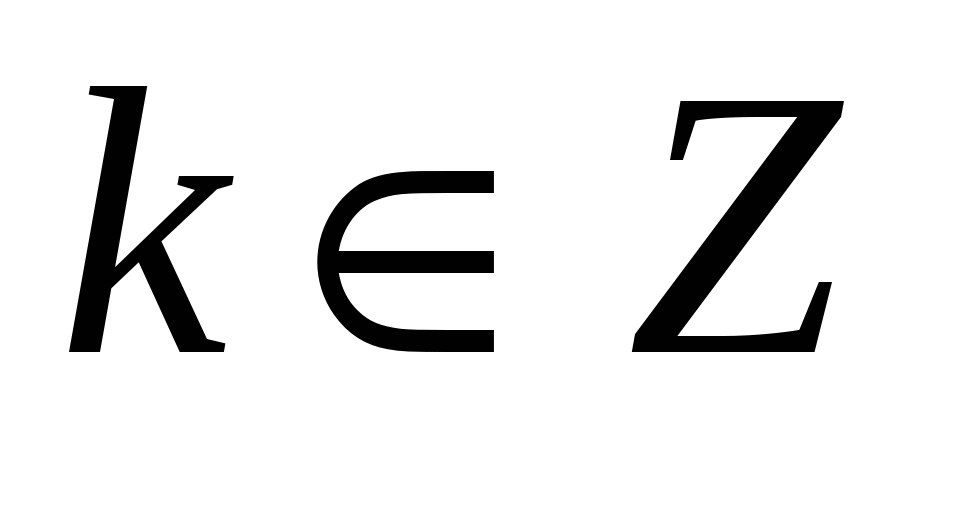; -arctg3 +πn,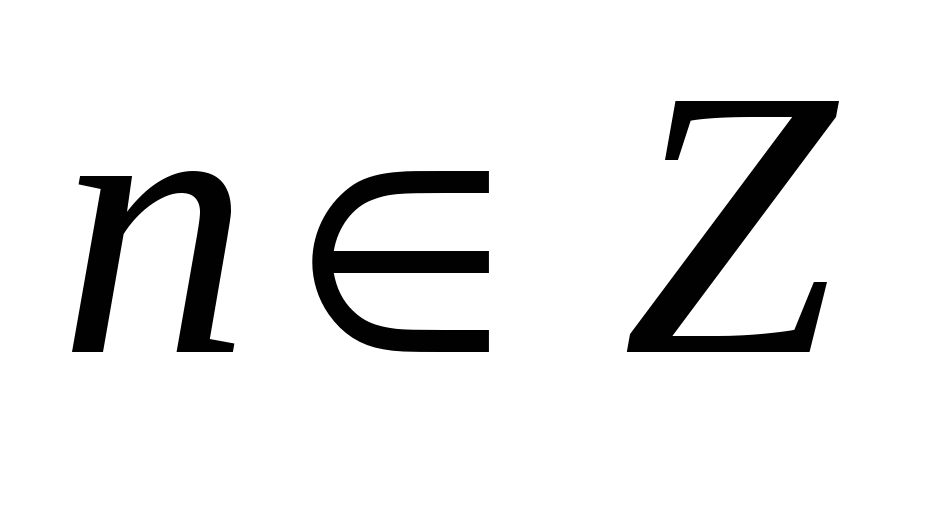

3. Решить №624 и №636(1,2)

4. Прислать решения 8.05 с 10.00 до 11.00

Желаю успехов!

12 Следующая ⇒