Аналитическая записка (задание 1)

Аналитическая записка (задание 1)

1. Расчет параметров уравнения линейной регрессии.

По нашим данным получим систему:

54657665,03a + 36389,1b = 2396177,22

36389,1a + 26b = 1727,6

Решая ее, найдем, что а = -0,00583; b = 74,607

Значит, уравнение регрессии имеет вид: y = -0,00583 x + 74,607

2. Оценка тесноты связи с помощью показателей корреляции и детерминации

Выборочная дисперсия s^2(x) = 2102217,886 - 1399,580769 х 1399,580769 = 143391,5562

Выборочное среднеквадратическое отклонение s(x) = 378,6707754

Выборочная дисперсия s^2(y) = 4421,593077 - 66,44615 х 66,44615 = 6,501715976

Выборочное среднеквадратическое отклонение s(y) = 2,549846265

Коэффициент корреляции r = (92160,66231 - 1399,580769 х 66,44615) / (378,6707754 * 2,549846265) = -0,865925996

Связь обратная, сильная.

Коэффициент детерминации = r^2 = 0,865925996^2 = 0,749827831

Вариация у на 75% объясняется вариацией х.

На долю прочих факторов приходится 25%

3. Оценка качества уравнения с помощью средней ошибки аппроксимации.

Средняя ошибка аппроксимации = 1,524%

Получили хорошее соответствие расчетных и фактических данных.

4. Определение статистической надежности результатов регрессионного моделирования с помощью F-критерия Фишера

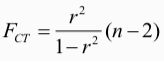
n=26

F_ст = 71,9339326

F_кр (0,05;1;24) = 4,26

71,9339326 > 4,26 => уравнение регрессии статистически значимо

5. Прогноз для у в виде доверительного интервала при х= 2000 и α=0,05

Рассчетное y_x = 2000*(-0,00583)+74,607 = 62,947

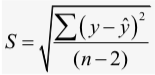
S = 1,32744

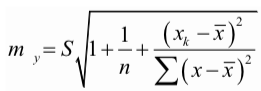
m_y = 1,41430479

Δy = t_st(0,05;24)*m_y = 2,064 * 1,41430479 = 2,91912509

Интервал: (62,947- 2,91912509; 62,947+ 2,91912509) или (60,0278749; 65,8661251)