Урок по теме: Показательная функция. Повторение 2-й курс 03.06.20

Урок по теме: "Показательная функция. Повторение" 2-й курс 03.06.20

Тип урока:урок повторения и обобщения

Цель урока: повторить и обобщить свойства показательной функции, а также методы решения показательных уравнений и неравенств.

закрепление знаний, умений и навыков студентов по данной теме;
применение свойств функции при решении уравнений и неравенств;

развитие логического мышления студентов и умения работать в проблемной

ситуации;

развитие умений сравнивать, обобщать, правильно формулировать задачи и

излагать мысли;

воспитание интереса и любви к предмету через содержание учебного материала,

умения работать в коллективе, взаимопомощи, культуры общения;

ХОД УРОКА:

Организационный момент.

Сегодня на уроке мы повторим и обобщим знания, связанные с понятием показательной функции, а также с понятием функции вообще. Проверим умение решать показательные уравнения и неравенства. Рассмотрим практическую значимость показательной функции, а также определим уровень усвоения материала по данной теме.

Задания с использованием свойств показательной функции, показательные уравнения и неравенства являются весьма популярными заданиями во всех вариантах тестов ЕГЭ и традиционно считаются трудной темой школьного курса математики.

«...Именно функция является тем средством
математического языка, которое позволяет
описывать процессы движения, изменения,
присущие природе».

Г.Галилей

Кто может ответить на вопрос, а что же такое функция? (Определение «функции»)

Функция – одно из основных математических общенаучных понятий, зависимость между переменными величинами.

Историческая справка.

Слово «функция» (от латинского function– исполнение, осуществление) в математике впервые употреблено немецким математиком В.Г.Лейбницем.

Но сами функции и способы их задания фактически изучались людьми очень давно. Знаменитый древнегреческий историк Геродот в 425 году до нашей эры писал, что египетские цари, разделив землю между египтянами, брали ежегодный налог, пропорциональный площади занимаемого участка. Конечно, ни египетские цари, ни землевладельцы, ни сам Геродот не произносили слова “функция”, но ведь речь идёт о том, что каждому значению площади соответствовало некоторое значение налога.

Хотя в древности функций не знали, но явления, которые мы сегодня описываем с их помощью, давно известны людям.

Какие ещё понятия связаны с понятием функции?

(повторить определения: зависимая переменная, независимая переменная, область определения, множества значений функции, график функции).

Понятие переменной величины было введено в науку франц. Ученым и математиком Рене Декартом.

Математика рассматривает абстрактные переменные величины, изучает различные законы их взаимосвязи, не углубляясь в природу задачи.

Например, в соотношении у = х² геодезист или геометр увидит зависимость площади квадрата от его стороны, а физик, авиаконструктор или кораблестроитель может усмотреть в нем зависимость силы у сопротивления воздуха или воды от скорости х движения.

Математика же изучает эту зависимость в отвлеченном виде, и она устанавливает, например, что увеличение х в 2 раза приведет к увеличению у в 4 раза, и это заключение может применяться в любой конкретной ситуации.

В курсе алгебры изучается немало функций. Одной из самых важных является показательная функция y=a^x, где a 0, a ≠ 1.

Графики показательной функции (Рисунок 1 и 2).

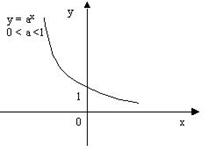
Рис. 1

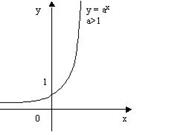
Рис. 2

Актуализация опорных знаний.

Почему ее называют показательной?
Чем отличаются степенная и показательная функции?

Еще 40 веков назад в египетском папирусе записан ряд. Про семь домов, где кошек 49, и каждая из них по 7 мышей съедает и тем всем столько зерен сохраняет, что мер 17000 составляет. Мы объяснили факт немножко, священна почему в Египте кошка.

О том еще известна нам легенда, что как-то у арабского царя
изобретатель шахматной доски, наверно потребовал за доску ту зерна. Причем за клетку первую – зерно, а за вторую – два просил изобретатель, за третью – снова больше раза в два, немало времени царь на подсчет потратил. Когда же подсчитали – прослезились: число двадцатизначно получилось! Хватило б зернами засеять нам всю сушу и миллионы лет пришлось зерно бы кушать.

Число е (экспонента).

Возведение в степень на немецком языке звучит - potenzie.Отсюда и происходит словопотенцировать.

А слово «показатель» на немецком языкезвучит какExponent.

Число е (экспонента) (от лат. exponens — показывающий) - одна из важнейших постоянных в математике.

Говорят, показательная кривая или (экспоненциальная) показательная функция.

Число е = .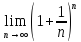

Обозначение e ввёл Леонард Эйлер в 1736 г. Он вычислил первые 23 знака этого числа в десятичной записи, а само число назвали в честь Непера «неперовым числом».

Число e играет особую роль в математическом анализе.

Показательная функция с основанием e, называется экспонентой и обозначается

12 Следующая ⇒