Доделать все работы и выслать мне на почту.

Доделать все работы и выслать мне на почту.

Кто не сделал эти задания, сделайте, точно такие будут на экзамене. Вариант 1

Часть 1

1.Пакет молока стоит 21 рубль 30 копеек. Какое наибольшее количество пакетов молока можно купить на 500 рублей?

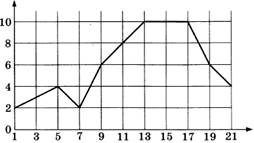
2. Первый посев семян петрушки рекомендуется проводить в апреле при дневной температуре воздуха не менее +6 °С. На рисунке показан прогноз дневной температуры воздуха на первые три недели апреля. Определите, в течение скольких дней за этот период можно производить посев петрушки.

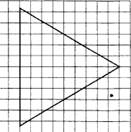
3. На клетчатой бумаге с размером клетки 1 х 1 изображён равносторонний треугольник. Найдите радиус вписанной в него окружности.

4. Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвуют 56 шашистов, среди которых 12 участников из России, в том числе Валерий Стремянкин. Найдите вероятность того, что в первом туре Валерий Стремянкин будет играть с каким-либо шашистом из России.

5. Найдите корень уравнения 5^{4 − х} = 25.

6. Отрезок АВ является хордой окружности с центром О. Найдите угол между прямой АВ и касательной к окружности, проходящей через точку А, если угол АОВ равен 56°. Ответ дайте в градусах.

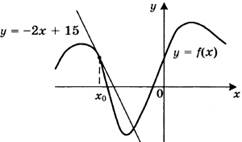
7. На рисунке изображены график функции у = f(х) и касательная к этому графику, проведённая в точке х₀. Касательная задана уравнением у = −2х + 15. Найдите значение производной функции

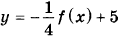
в точке х₀.

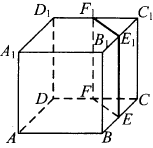
8. В кубе АВСDA₁B₁C₁D₁ точки Е, F, E₁ и F₁ являются серединами рёбер BC, DC, B₁C₁ и D₁C₁соответственно. Объём призмы, отсекаемой от куба плоскостью EFF₁, равен 14. Найдите объём куба.

Часть 2

9. Найдите значение выражения (558² − 23²) : 581.

10. Ёмкость высоковольтного конденсатора в телевизоре С = 4 · 10⁻⁶ Ф. Параллельно с конденсатором подключён резистор с сопротивлением R = 2 · 10⁶ Ом. Во время работы телевизора напряжение на конденсаторе U₀ = 22 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением

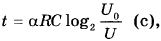
где α = 1,7 с / Ом · Ф - постоянная. Определите напряжение на конденсаторе, если после выключения телевизора прошло 27,2 секунды. Ответ дайте в кВ (киловольтах).

11. В сосуд, содержащий 7 литров 15-процентного водного раствора некоторого вещества, добавили 8 литров воды. Сколько процентов составит концентрация получившегося раствора?

12. Найдите наибольшее значение функции

у = (21 − х)е^{х − 20}

на отрезке [19; 21].

13. Решите уравнение

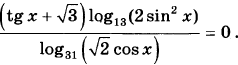
14. В правильной четырёхугольной пирамиде SABCD с вершиной S сторона основания равна 4. Точка L - середина ребра SC. Тангенс угла между прямыми BL и SA равен

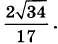
а) Пусть О - центр основания пирамиды. Докажите, что прямые BO и LO перпендикулярны.

б) Найдите площадь поверхности пирамиды.

15. Решите неравенство

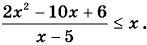
16. Окружность с центром О вписана в угол, равный 60°. Окружность большего радиуса с центром О₁также вписана в этот угол и проходит через точку О.

а) Докажите, что радиус второй окружности вдвое больше радиуса первой.

б) Найдите длину общей хорды этих окружностей, если известно, что радиус первой окружности равен 2√3.

17. В двух областях есть по 90 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,3 кг алюминия или 0,1 кг никеля. Во второй области для добычи х кг алюминия в день требуется х² человеко-часов труда, а для добычи у кг никеля в день требуется у² человеко-часов труда.

Для нужд промышленности можно использовать или алюминий, или никель, причём 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую массу металлов можно добыть в двух областях суммарно для нужд промышленности?

18. Найдите все значения параметра а, при каждом из которых неравенство

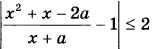
не имеет решений на интервале (1; 2).

19. Решите в целых числах уравнение 3ⁿ + 8 = x².

Вариант 2

Часть 1

1. Для покраски потолка требуется 140 г краски на 1 м². Краска продаётся в банках по 3 кг. Какое наименьшее количество банок краски нужно купить для покраски потолка площадью 42 м²?

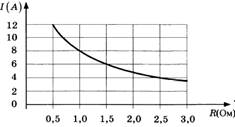
2. Мощность отопителя в автомобиле регулируется дополнительным сопротивлением, которое можно менять, поворачивая рукоятку в салоне машины. При этом меняется сила тока в электрической цепи электродвигателя - чем меньше сопротивление, тем больше сила тока и тем быстрее вращается мотор отопителя. На рисунке показана зависимость силы тока от величины сопротивления. На оси абсцисс откладывается сопротивление (в Омах), на оси ординат - сила тока в Амперах. Ток в цепи электродвигателя уменьшился с 8 до 4 Ампер. На сколько Омов при этом увеличилось сопротивление цепи?

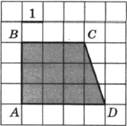
3. Найдите площадь трапеции ABCD, изображённой на клетчатой бумаге с размером клетки 1 х 1 (см. рис.).

4. Конкурс исполнителей проводится в 3 дня. Всего заявлено 80 выступлений - по одному от каждой страны. В первый день запланировано 20 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?

5. Решите уравнение log₂₅(2 − 3х) = 0,5.

6. В треугольнике АВС углы А и В равны соответственно 45° и 67°. Найдите угол между биссектрисой и высотой, проведёнными из вершины С. Ответ дайте в градусах.

7. На рисунке изображён график функции у = f(x). Прямая, проходящая через точку (−1; 1), касается этого графика в точке с абсциссой 3. Найдите f(3).

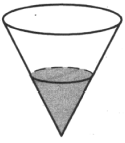
8. В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём жидкости равен 25 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

Часть 2

9. Найдите cos α, если

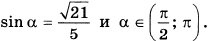
10. Высоту над землей (в метрах) подброшенного вверх камня можно вычислять по формуле h(t) = 1,4 + 14t − 5t², где t - время в секундах. Сколько секунд камень будет находиться на высоте более 8 метров?

11. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 60 км/ч, а вторую половину времени - со скоростью 46 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

12. Найдите точку минимума функции у = х³ − 12х² + 15.

13. а) Решите уравнение

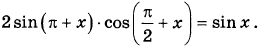
б) Найдите все корни этого уравнения, принадлежащие отрезку [−5п; −4п].

14. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ стороны основания равны 5, а боковые рёбра равны 11.

а) Докажите, что прямые СА₁ и C₁D₁ перпендикулярны.

б) Найдите площадь сечения призмы плоскостью, проходящей через вершины С, А₁ и F₁.

15. Решите неравенство

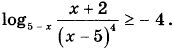
16. Две окружности касаются внутренним образом. Третья окружность касается первых двух и их линии центров.

а) Докажите, что периметр треугольника с вершинами в центрах трёх окружностей равен диаметру наибольшей из этих окружностей.

б) Найдите радиус третьей окружности, если известно, что радиусы первых двух равны 3 и 2.

17. 31 декабря 2014 года Олег взял в банке некоторую сумму в кредит под некоторый процент годовых. Схема выплаты кредита следующая - 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на а%), затем Олег переводит очередной транш. Если он будет платить каждый год по 328050 рублей, то выплатит долг за 4 года. Если по 587250 рублей, то за 2 года. Найдите а.

18. Найдите все значения а, при каждом из которых уравнение

8х⁶ + 4х² = (3х + 5а)³ + 6х + 10а

не имеет корней.