класс Лабораторная работа «Проверка закона изобарного процесса Гей-Люссака»

10 класс Лабораторная работа «Проверка закона изобарного процесса Гей-Люссака»

2.02. Проверка закона изобарного процесса Гей-Люссака

Установка моделирует лабораторную работу «Проверка закона изобарного процесса Гей-Люссака».

Цель работы:экспериментальным путем проверить верность закона Гей-Люссака (доказать постоянную V/T).

Краткая теория

В 1802 году, французский ученый Жозеф Луи Гей-Люссак опубликовал закон определяющий зависимость объёма газа от температуры при постоянном давлении и неизменной массе. Изобарный процесс - это процесс при котором изменяется состояние термодинамической системы при постоянном давлении. Если переводить с греческого то дословно получается: isos – равный и baros – тяжесть, вес. Стеклянный сосуд заполнен определенным газом, и этот сосуд присоединен к продолговатой стеклянной трубке. Каплей ртути закупорен газ в этой трубке. В следствии того, что трубка находится в горизонтальном расположении, давление в сосуде постоянно остаётся равным атмосферному. Температура газа увеличивается от 0 до 100°С. Увидеть изменение объёма можно при помощи капельки ртути, которая будет перемещаться по стенке стеклянной трубки. Гей-Люссак измерял объём газа в интервале температур от 0 до 100°С. Исследуя различные газы он получил для них следующие значения температурного коэффициента объёмного расширения α = (V – V₀ )/ V₀ · t:

Таблица 2.1. Температурный коэффициент объемного расширения газов

Газ	Температурный коэффициент объёмного расширения, 1/°С
Воздух	0,003671
Водород	0,003661
Окись азота	0,003720
Циан	0,003877
СО₂	0,003710
СО	0,003669
S О₂	0,003903

Получив такие данные, Гей-Люссак сделал следующие выводы:

а) при одинаковом повышении температуры, все газы и пары одинаково расширяются;

б) для всех газов увеличение объёма в интервале температур от температуры таяния льда до температуры кипения воды равно 100/26666 первоначального объёма.

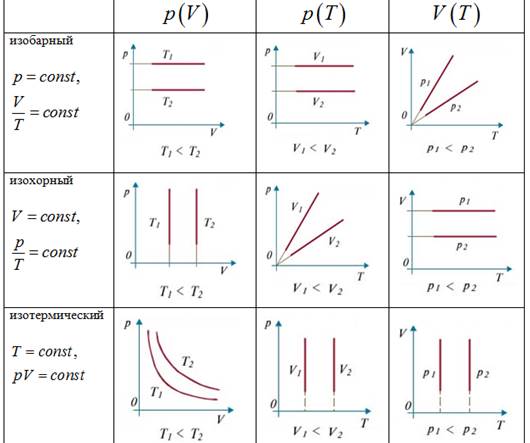
Таким образом, на основании наблюдений Гей-Люссак установил закон: относительное изменение объёма газа данной массы при постоянном давлении прямо пропорционально изменению температуры t. (V – V₀)/V₀ = a×t, где a – температурный коэффициент объёмного расширения, численно равный относительному изменению объёма газа при изменении его температуры на 1 градус. Опыт показывает, что при малых плотностях коэффициент объёмного расширения одинаков для всех газов: a = 1/273 1/°С. С точки зрения МКТ этот факт объясняется тем, что молекулы газа находятся в среднем на больших расстояниях друг от друга, и особенности межмолекулярных сил для различных газов в этих условиях не сказываются. Закон можно записать в виде: V = V₀(1 + αt). Объём данной массы газа при постоянном давлении меняется линейно при изменении температуры.

Если продолжить изобару в область низких температур, где измерения не проводились, то прямая пересекает ось температуры в точке, соответствующей объёму, равному нулю. Однако, это еще не значит, что объём газа действительно обращается в ноль. Ведь все газы при сильном охлаждении превращаются в жидкости, а к жидкостям ни закон Бойля – Мариотта, ни закон Гей-Люссака не применимы. Реальные газы подчиняются основным газовым законам лишь приближённо и тем менее точно, чем больше плотность газа и ниже его температура. Газ, который в точности подчиняется газовым законам, называют идеальным.

В молекулярно-кинетической теории модель «идеальный газ» удовлетворяет следующим требованиям:

1. объём всех молекул газа много меньше объёма сосуда;

2. силы притяжения между молекулами малы, и ими пренебрегают;

3. молекулы взаимодействуют только при соударении (удар упругий), при этом действуют силы отталкивания;

4. время столкновения много меньше времени между столкновениями.

Тот факт, что численное значение температурного коэффициента объёмного расширения в предельном случае малых плотностей одинаково для всех газов, позволяет установить температурную шкалу, не зависящую от вещества, – идеальную газовую шкалу температур.

Взяв за основу шкалу Цельсия, можно определить температуру из соотношения: t = (V – V₀)/V₀, где V – объём газа при 0°С, а V – его объём при температуре t. Так осуществляется определение температуры, не зависящее от вещества термометра.

Предельную температуру, при которой объём идеального газа становится равным нулю, принимают за абсолютный нуль температуры. Найдём значение абсолютного нуля по шкале Цельсия. Приравнивая объём V к нулю и учитывая, что α = 1/273 1/°С, получим: 0 = V₀(1 + 1/273×t). И получаем, что абсолютный нуль температуры равен: t = – 273°С. Это предельная, самая низкая температура в природе, та «наибольшая или последняя степень холода», существование которой предсказал Ломоносов.

Такой учёный как Уильям Кельвин из Англии, ввёл абсолютную шкалу температур. Нулевая температура по шкале Кельвина равна абсолютному нулю, а единица температуры по этой шкале - градусу по шкале Цельсия, из за этого абсолютная температура Т связана с температурой по шкале Цельсия формулой: Т = t + 273°С, причём 1°С = 1 К. Если посмотреть с точки зрения молекулярно - кинетической теории, то получается, что Т = 0 К, и тепловое движение молекул прекращается.

С помощью шкалы Кельвина, закон Гей-Люссака можно записать проще:

1 + α×t = 1 + 1/273(T – 273) = α×T, тогда V = V₀×α×T.

Объём газа данной массы при постоянном давлении прямо пропорционален абсолютной температуре.

Следовательно отношение объёмов газа одной и той же массы в различных состояниях при постоянном давлении равно отношению абсолютных температур: V₁/ V₂ = Т₁/ Т₂.

Таблица 2.2. Характеристики изобарного процесса

Постоянный параметр	Название изопроцесса	Связь между другими параметрами	Объяснение связи между параметрами с точки зрения МКТ
Р = const при m= cost.	Изобарный процесс (закон Гей-Люссака, 1802 год).	V / T = const; V₁ /Т₁ = V₂/ Т₂; V₁ / V₂ = Т₁/ Т₂.	Рост температуры означает увеличение средней кинетической энергии теплового движения молекул газа. Чтобы поддерживать давление постоянным, необходимо не допустить увеличения числа ударов о единицу площади поверхности стенки

12 Следующая ⇒