Зачет по теме: « Линейная функция и её график»

Зачет по теме: « Линейная функция и её график»

(Часть 1)

1.Какая из данных функций является линейной?

1) у = -2,8х²- 5,4х + 11,2 ; 3) у = ;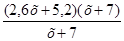

2) у = 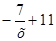; 4) у = .

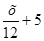2. Для функции у = 2 – 8х найдите k и b. Как называют k?

3. Функции заданы формулами. Какая из функций является прямой

пропорциональностью?

1) у = x + 5; 3) у = 3 – x;

2) у = 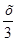; 4) у = .

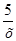4. Графиком какой из данных функций является прямая, проходящая через

начало координат?

1) у = 20 + x; 3) у = 20х;

2) у = 20 – x; 4) у = x – 20.

5. Угол, который прямая у = kx образует с положительным направлением

оси OX, зависит от ____________________________. Если k > 0, то

этот угол _______________, если k < 0, то угол _____________________.

6. Задайте формулой прямую пропорциональность, график которой

параллелен графику функции у = -2х + 4. В каких координатных

четвертях расположен её график?

7. Как выяснить пересекаются ли графики функций, заданных формулами

у = 0,9х – 1 и у = 0,8х + 1.

8. Укажите формулу, задающую линейную функцию, график которой

параллелен оси OX:

а) у = 6х; б) у = х – 7; в) у = - 5.

Ответы: 1) а и б; 2) в; 3) а; 4) б.

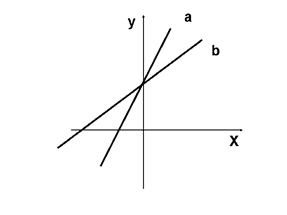
9. Укажите функцию, изображенную на

рисунке.

1) у = - 0,5х – 2; 3) у = 0,5х – 2;

2) у = 0,5х + 2; 4) у = - 0,5х +2.

10. Не выполняя построений и вычислений,

определите, графики каких функций

изображены на рисунке.

1) (а) у = -0,8х + 4, 3) (а) у = -3х + 3,

(b) у = 2х + 4; (b) у = 3х + 2;

2) (а) у = 3х + 2, 4) (а) у = 2х + 4,

(b) у = 3х + 3; (b) у = 0,8х + 4.

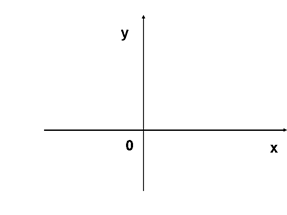
11. Изобразите схематично график

линейной функции, для

которой выполнены условия:

(Часть 2)

1. Постройте график функции у = 3х – 5

и найдите координаты точек

пересечения графика с осями

координат.

2. Найдите координаты точек

пересечения графиков функций

у = 5х -9 и у = -2х + 12.

3. Постройте график функции у = .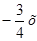

Пользуясь графиком, найдите:

а) значение функции, если значение

аргумента равно 8;

б)значение аргумента, при котором

значение функции равно -3.

4. График функции у = ax + а + 5 проходит

через точку В( 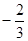; -1).

Найдите значение а.