Изучение дифракции света. Дифракция света

Министерство образования Республики Беларусь Учреждение образования Международный государственный экологический университет им. А.Д. Сахарова

Факультет мониторинга окружающей среды

Кафедра физики и высшей математики

Лабораторная работа № 4.03

Изучение дифракции света

Минск

2014

Дифракция света

Цель работы:изучение дифракции Фраунгофера на дифракционной решетке

Приборы и принадлежности:лазер, дифракционная решетка, оптическая скамья, экран, блок питания лазера.

Теоретическое введение:

Дифракцией света называется совокупность оптических явлений, обусловленных волновой природой света и наблюдающихся при его распространении в среде с резко выраженными неоднородностями (например, при прохождении через отверстия в экранах, возле границ непрозрачных тел и т.д.). В более узком смысле под дифракцией понимают огибание светом малых препятствий, т.е. отклонение от законов геометрической оптики, которое ведет к проникновению света в область геометрической тени и интерференционным явлениям, сопровождающим это отклонение. Дифракция наблюдается при при условии, что 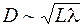, где размеры неоднородности, 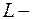расстояние от неоднородности до точки наблюдения, 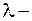длина световой волны.

Если источник света и точка наблюдения находятся на большом расстоянии от преграды, то лучи, падающие на преграду и идущие от нее, создают практически параллельные пучки. В этом случае имеет место дифракция в параллельных лучах или дифракция Фраунгофера.

Дифракция Фраунгофера также может быть осуществлена, если поместить источник света в фокусе собирающей линзы, установленной перед препятствием, а дифракционную картину наблюдать на экране, установленном в фокальной плоскости второй собирающей линзы, расположенной за препятствием. При использовании в качестве источника света лазера, собирающая линза перед препятствием не требуется, так как лучи светового пучка лазера практически параллельны.

Дифракция Френеля – это дифракция в сходящихся лучах. В этом случае на препятствие падает сферическая или плоская волна, а дифракционная картина наблюдается на экране, находящемся за препятствием на достаточно близком расстоянии от него.

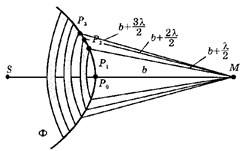Точный расчет дифракционной картины представляет собой очень сложную математическую задачу. Но в ряде практически важных случаев достаточно хорошие результаты дает упрощенный способ, расчета дифракционной картины основанный на принципе Гюйгенса-Френеля. В соответствии с этим принципом каждая точка волнового фронта является источником вторичных волн, которые распространяются по всем направлениям. Эти волны когерентны, потому что все они возбуждаются одним и тем же первичным источником. Световое поле, возникшее в результате их интерференции, в пространстве вне этой поверхности совпадает с полем реального источника света, а амплитуда и фаза волны в любой точке пространства определяются как результат интерференции вторичных волн. Таким образом, реальный источник света заменяется световой поверхностью вокруг него, с непрерывно распределенными по этой поверхности когерентными вторичными источниками. Отличие этой поверхности от реальной поверхности излучающего тела состоит в том, что она абсолютно прозрачна для всякого излучения.

Рис.1

Для нахождения результата интерференции вторичных волн Френель предложил метод разбиения волнового фронта на кольцевые зоны, называемые зонами Френеля. Поверхность падающей волны, разбивают на зоны такого размера, чтобы расстояния от краев зоны до точки М, в которой определяется интенсивность света (рис. 1), отличались на половину длины волны. Колебания, которые приходят в точку М от эквивалентных точек двух соседних зон (т.е. от точек, лежащих возле внешних краев зон или внутри зон и т.д.), совершаются в противофазе, т.е. в результате интерференции будут ослаблять друг друга. Поэтому амплитуда результирующего светового колебания в точке М

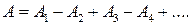. Пока отрывается первая зона Френеля интенсивность света в точке М увеличивается и достигает максимума при полностью открытой зоне. По мере открытия второй зоны Френеля интенсивность уменьшается и при полностью открытой второй зоне уменьшается почти до нуля. Это обусловлено тем, что амплитуда колебаний, которые возбуждает каждая следующая зона в точке М, уменьшается с увеличением угла между нормалью к поверхности зоны и направлением на точку М. По мере открытия третьей зоны интенсивность будет опять увеличиваться и т.д.

Френель предположил также, что действие отдельных зон в точке М зависит от направления распространения (от угла φ (рис. 17.19) между нормалью n к поверхности зоны и направлением на точку М). С увеличением φ_т действие зон убывает и при углах φ_т > 90° амплитуда возбуждаемых вторичных волн равна 0. Кроме того, интенсивность излучения в направлении точки М уменьшается с ростом т и вследствие увеличения расстояния до точки М. Поэтому

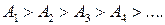
Дифракционной решеткой называют оптический прибор, представляющий собой совокупность большого количества параллельных штрихов одинаковой формы, нанесенных на плоскую или вогнутую полированную поверхность на одинаковом расстоянии друг от друга. Различают прозрачные и отражающие дифракционные решетки. В прозрачных дифракционных решетках штрихи наносятся на поверхность полированной прозрачной пластинки (обычно стеклянной), и наблюдение дифракции ведется в проходящем свете. В отражающих дифракционных решетках штрихи наносятся на зеркальную (обычно металлическую) поверхность, и наблюдение ведется в отраженном свете.

Рис.2

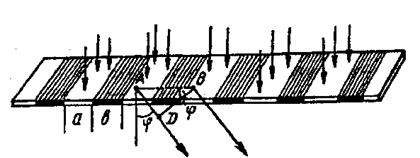
Плоская прозрачная дифракционная решетка

(рис. 2), представляет собой периодическую структуру, состоящую из параллельных друг другу прозрачных участков (щелей) шириной 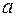, которые разделены между собой непрозрачными участками (штрихами) шириной 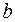. Сумма 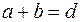называется периодом (или постоянной) дифракционной решетки. Пусть на эту решетку падает плоская монохроматическая световая волна, направление распространения которой перпендикулярно плоскости решетки. В результате дифракции на узких щелях решетки после нее световые волны распространяются во всех возможных направлениях, т.е. под любым углом 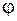к направлению распространения падающей волны, поскольку щели решетки являются длинными и узкими вторичными источниками света. Так как эти источники освещаются одной световой волной, то они являются когерентными, в результате чего волны, излучаемые ими, интерферируют друг с другом. Если за решеткой поместить собирающую линзу, в фокальной плоскости которой находится экран, то в каждой точке экрана соберутся те лучи, которые до линзы были параллельными и распространялись под определенным углом j к направлению волны, падающей на решетку (рис. 3). Поэтому интенсивность света в точке наблюдения В определяется результатом интерференции вторичных волн, распространяющихся как от разных участков

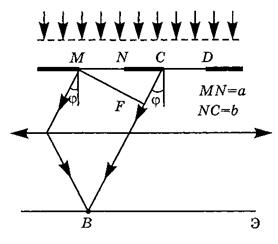одной щели, так и от разных щелей. Поскольку линза не вносит дополнительной разности хода для лучей, падающих на нее параллельным пучком, то колебания, складывающиеся в точке Р, имеют такую же разность хода, что и до линзы ( в плоскости, перпендикулярной этим лучам).

Рис.3

Если разность хода между вторичными волнами, которые распространяются из эквивалентных точек соседних щелей, равна четному числу полуволн, т. е.

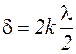, то в точке В будет наблюдаться дифракционный максимум. Для определения положения дифракционных максимумов рассмотрим эквивалентные точки М и С соседних щелей решетки, которые находятся на одинаковых расстояниях от левых (или правых) краев своих щелей и расположены в одной плоскости, параллельной плоскости рисунка. Расстояние между такими точками

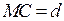. По условию точки М и С колеблются в одинаковой фазе. От перпендикулярной лучам плоскости решетки до встречи в фокальной плоскости линзы отношения этих фаз не изменяются, значит, разность хода лучей определяется длиной отрезка CF. Из рис. 3 видно, что

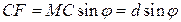Поэтому условие дифракционного максимума может быть записано в виде: 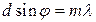. Максимумы, которые наблюдаются под углами , называются главными, а полученная формула называется формулой дифракционной решетки. Максимум, соответствующий углу 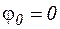, называется максимумом нулевого порядка 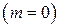. Значение угла, которое удовлетворяет условию 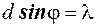, соответствует главному максимуму первого порядка 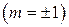и т. д. Причем главные максимумы, соответствующие положительным и отрицательным значениям 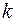, располагаются на экране симметрично относительно максимума нулевого порядка.

Главные минимумы наблюдаются на экране под такими углами дифракции 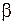, для которых свет от разных частей каждой щели полностью гасится в результате интерференции. Эти углы определяются из соотношения .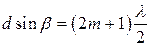

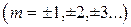Из формулы дифракционной решетки следует, что нулевой максимум будет в точке 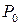, расположенной на оси симметрии независимо от длины волны (при 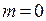, , 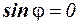т.е. 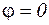независимо от длины волны). Все другие максимумы отклоняются от нулевого тем больше, чем больше длина волны для одного и того же максимума, причем 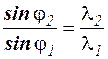, а при малых углах 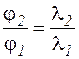. Поэтому при падении на дифракционную решетку белого света на экране наблюдается его разложение в дифракционный спектр. Причем максимум нулевого порядка (спектр нулевого порядка) представляет собой неокрашенное изображение источника света (щели). Максимумы первого, второго и т. д. порядков растягиваются в цветные полоски, внутренний край которых (край, обращенный к максимуму нулевого порядка) окрашен в фиолетовый цвет, а внешний ‑ в красный. Это обусловлено тем, что чем меньше длина световой волны, тем меньшему значению угла соответствует положение главного максимума.

12 Следующая ⇒