
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вариант № 8. Список литературы
| САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени Гагарина Ю.А. Институт __ИнЭТМ________ Курс_________2____________ Специальность__б-ИКТСипу21____ Шифр_______182888________ Вариант______8_________ Контрольная/курсовая работа №___________________1_______________________ по _________дискретной математике___________________ (наименование дисциплины) На тему____________________________________________ (полное название темы или номер варианта) Студента Краева Алексея Валерьевича______ (фамилия, имя и отчество полностью) ___________________________________________ Дата отправки работы Отметка о зачете работы: в университет_______________________________________ Дата регистрации работы_____________________________ в университете ______________________________________ ______________________________________ |
Вариант № 8
1. В третьем семестре изучаются 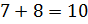 дисциплин. Сколькими способами можно составить расписание на какой-либо день недели, если в этот день должны быть четыре пары по различным дисциплинам?
дисциплин. Сколькими способами можно составить расписание на какой-либо день недели, если в этот день должны быть четыре пары по различным дисциплинам?
Решение:
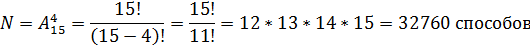
Ответ: 32760 способов.
2. Сколько шестизначных чисел, кратных пяти, можно составить из цифр 1, 2, 3, 4, 5, 6 при условии, что цифры в числе не повторяются.
Решение:
В нашем случае число кратно пяти, если оно заканчивается цифрой 5. Требуется расставить 5 цифр (1, 2, 3, 4, 6) на первые пять разрядов шестизначного числа. Используем перестановки без повторений: 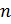 различных элементов можно расположить на
различных элементов можно расположить на 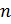 местах
местах 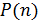 способами – число перестановок без повторений из
способами – число перестановок без повторений из 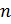 элементов:
элементов:
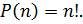
Значит,
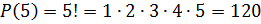
Ответ: 120 шестизначных чисел, кратных пяти.
3. В чемпионате по футболу участвуют 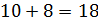 команд, причем каждые две команды встречаются друг с другом дважды. Сколько матчей будет проведено?
команд, причем каждые две команды встречаются друг с другом дважды. Сколько матчей будет проведено?
Решение:
Каждая из 18 команд играет дважды с 17 командами, значит проводит 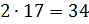 матчей. Учитывая, что команды играют друг с другом, всего будет проведено
матчей. Учитывая, что команды играют друг с другом, всего будет проведено
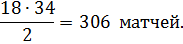
Ответ: 306 матчей.
4. Найти выражение для суммы первых 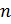 «треугольных» чисел (написать формулу для
«треугольных» чисел (написать формулу для 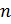 – го «треугольного» числа):
– го «треугольного» числа):
1, 3, 6, 10, 15, 21, 28,…
Решение:
Пусть 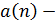 треугольное число, тогда
треугольное число, тогда
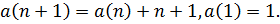
Решим уравнение:
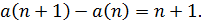
Характеристическое уравнение
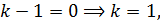
значит, решение уравнения
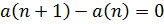
имеет вид
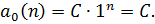
Подберем частное решение исходного уравнения в виде
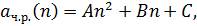
тогда
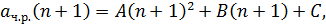
подставляем:
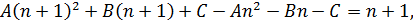
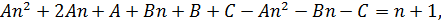
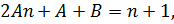
откуда
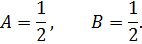
Таким образом,
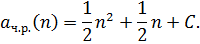
Так как 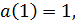 то
то
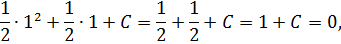
откуда 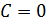 и искомая формула для треугольного числа
и искомая формула для треугольного числа

Пусть 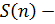 сумма первых
сумма первых 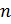 треугольных чисел, тогда
треугольных чисел, тогда
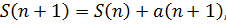
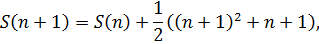
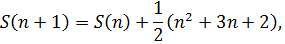
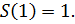
Решаем характеристическое уравнение:
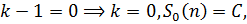
частное решение
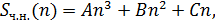
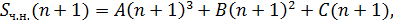
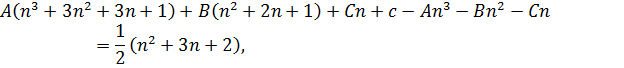
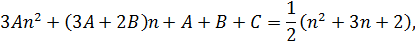
откуда
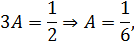
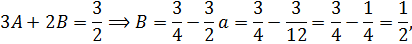
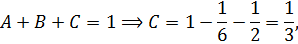
значит,
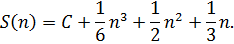
Так как
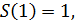
то
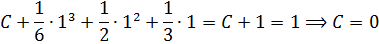
и
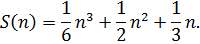
5. Последовательность Фибоначчи задаётся рекуррентным соотношением 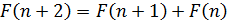 и начальными условиями
и начальными условиями 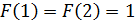 . Найти выражение для общего члена последовательности и выписать её первые 18 членов.
. Найти выражение для общего члена последовательности и выписать её первые 18 членов.
Решение:
Составляем характеристическое уравнение:

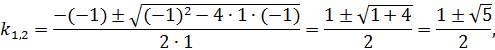
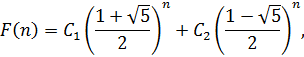
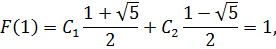
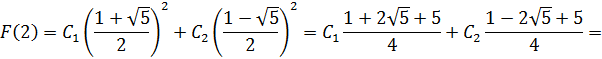
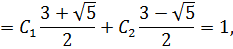
составим и решим систему
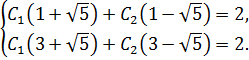
Вычтем из первого уравнения второе:
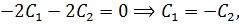
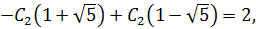
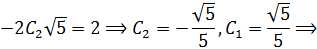
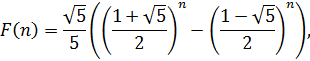
Тогда
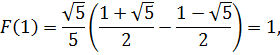
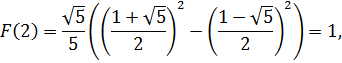
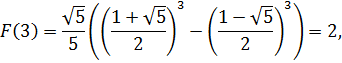
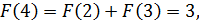
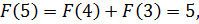
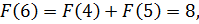
и так далее. Представим в виде таблицы первые 18 членов:
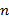
| ||||||||||||||||||
|
Задание 5.6.1. Найти общее решение рекуррентного соотношения 5-го порядка:
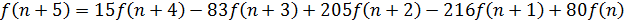
Характеристическое уравнение заданного соотношения:
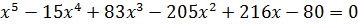
Непосредственной подстановкой убеждаемся 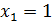 – корень характеристического уравнения.
– корень характеристического уравнения.
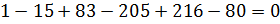
Понижаем степень характеристического уравнения для чего делим его на:
(х-1)
Выделяем множитель 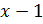 :
:
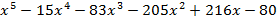
| 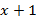
|

| 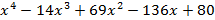
|

| |

| |

| |
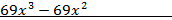
| |
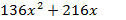
| |
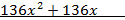
| |
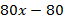
| |
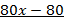
| |
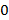
|
В результате деления получим уравнение 4-ой степени
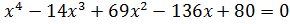
Заметим, что 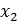 =1 также является его корнем, разделим левую часть уравнения (х-1)
=1 также является его корнем, разделим левую часть уравнения (х-1)
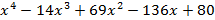
| 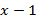
|

| 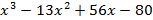
|
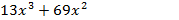
| |
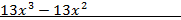
| |
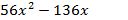
| |
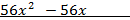
| |
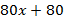
| |
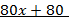
| |
|
И получим:
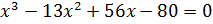
Корнем этого уравнения 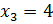 , поэтому поделим этот множитель на (x-4).
, поэтому поделим этот множитель на (x-4).
Выделяем множитель 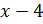 :
:
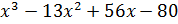
| 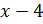
|

| 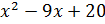
|
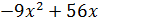
| |
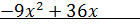
| |
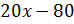
| |
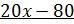
| |
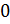
|
Таким образом,
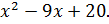
Решаем квадратное уравнение
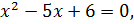
Его дискриминант равен: 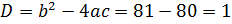
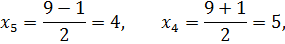
таким образом, характеристическое уравнение представляется в виде:
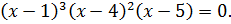
Действительному корню 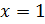 кратности 2 соответствуют решение.
кратности 2 соответствуют решение.
Действительному корню 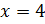 кратности 1 соответствует решение.
кратности 1 соответствует решение.
Действительному корню 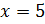 кратности 1 соответствует решение.
кратности 1 соответствует решение.
Все эти 5 решений – линейно независимые и общее решение заданного рекуррентного соотношения 5-го порядка является линейной комбинацией этих пяти решений:
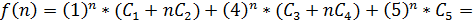
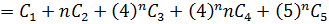
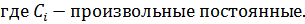
Список литературы
1. Акимов, О.Е. Дискретная математика. Логика, группы, графы / О.Е. Акимов. - М.: Бином. Лаборатория знаний, 2009. - 376 c.
2. Акимов, О.Е. Дискретная математика. Логика, группы, графы / О.Е. Акимов. - М.: Бином. Лаборатория знаний, 2003. - 376 c.
3. Андерсон, Дж. Дискретная математика и комбинаторика / Дж. Андерсон. - М.: Диалектика, 2019. - 960 c.
4. Асанов, М.О. Дискретная математика: графы, матроиды, алгоритмы: Учебное пособие / М.О. Асанов, В.А. Баранский, В.В. Расин. - СПб.: Лань, 2010. - 368 c.
5. Бабичева, И.В. Дискретная математика. Контролирующие материалы к тестированию: Учебное пособие / И.В. Бабичева. - СПб.: Лань, 2013. - 160 c.
6. Баврин, И.И. Дискретная математика для педагогических вузов: Учебник и задачник для прикладного бакалавриата / И.И. Баврин. - Люберцы: Юрайт, 2015. - 208 c.
7. Баврин, И.И. Дискретная математика: Учебник и задачник для СПО / И.И. Баврин. - Люберцы: Юрайт, 2016. - 209 c.
8. Вороненко, А.А. Дискретная математика. Задачи и упражнения с решениями: Учебно-методическое пособие / А.А. Вороненко. - М.: НИЦ Инфра-М, 2013. - 104 c.
9. Вороненко, А.А. Дискретная математика. Задачи и упр. с реш.: Учебно-методическое пособие / А.А. Вороненко, В.С. Федорова. - М.: Инфра-М, 2018. - 160 c.
10. Галкина, В.А. Дискретная математика: комбинаторная оптимизация на графах / В.А. Галкина. - М.: Гелиос АРВ, 2003. - 232 c.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|