
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Примерный перечень задач, выносимых на экзамен
Вопросы к экзамену
в летнюю сессию 1 курс, 2 семестр
для студентов заочного обучения направления подготовки 13.03.02 Электроэнергетика и электротехника, 13.03.01 Теплоэнергетика и теплотехника
1. Исследование функции на монотонность
2. Экстремум функции. Необходимое условие экстремума. Правило исследования на экстремум с помощью первой производной.
3. Выпуклость, вогнутость. Точки перегиба. Правило отыскания точек перегиба с помощью второй производной.
4. Асимптоты.
5. Общая схема исследования функции.
6. Понятие первообразной и неопределенного интеграла.
7. Простейшие приемы интегрирования:
а) метод непосредственного интегрирования
б) замена переменной
в) интегрирование по частям.
8. Простейшие дроби и методы их интегрирования.
9. Интегрирование дробно-рациональной функции.
10. Суть метода неопределенных коэффициентов при разложении правильной дроби в сумму простейших дробей.
11. Интегрирование иррациональных выражений вида 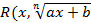 ),
), 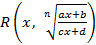
12. Интегрирование тригонометрических выражений.
13. Определение интеграла через интегральную сумму.
14. Формула Ньютона-Лейбница.
15. Основные свойства определенного интеграла.
16. Интегрирование по частям и замена переменной в определенном интеграле.
17. Геометрический смысл определенного интеграла.
18. Вычисление площадей в декартовых и полярных координатах.
19. Вычисление длины дуги в декартовых, полярных координатах и заданной параметрически.
20. Вычисление объемов тел с помощью определенного интеграла.
21. Несобственные интегралы с бесконечными пределами интегрирования.
22. Несобственные интегралы от неограниченных функций.
23. Понятие частных производных первого порядка.
24. Дифференцирование сложных функций.
25. Понятие дифференцируемости функции двух переменных.
26. Полный дифференциал. Инвариантная форма первого дифференциала.
27. Правила дифференцирования неявных функций.
28. Уравнения касательных плоскостей и нормалей.
29. Производная по направлению. Градиент функции.
30. Понятие экстремума функции двух переменных. Необходимое условие экстремума. Достаточное условие экстремума для функций двух переменных.
31 Понятие двойного интеграла.
32. Повторные интегралы. Способы вычисления двойных интегралов через повторные для прямоугольных и криволинейных областей интегрирования.
33. Замены переменных в двойном интеграле. Формула вычисления двойного интеграла в полярных координатах.
34. Применение двойного интеграла к вычислению объемов тел.
35. Понятие числового ряда и его суммы.
36. Необходимое условие сходимости. Геометрический и гармонические ряды.
38. Признак сравнения. Принцип сравнения в предельной форме.
39. Признак Даламбера.
40. Признак Коши.
41. Интегральный признак Коши.
42. Обобщенный гармонический ряд.
43. Знакочередующийся ряд. Теорема Лейбница.
44. Абсолютно и условно сходящиеся знакопеременные ряды.
45. Свойства абсолютно сходящихся рядов.
46. Признаки абсолютной сходимости.
Примерный перечень задач, выносимых на экзамен
1. Найти интегралы.
а) 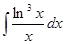 , б)
, б) 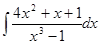 , в)
, в) 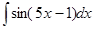
2. Вычислить интеграл, выполнив замену переменной
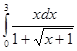
3. Вычислить площадь фигуры, ограниченной линиями
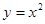 и
и 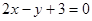
4. Найти производные, используя формулы дифференцирования сложных функций:
1) 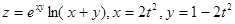 ,
, 
2) 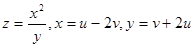 ,
, 
5. 1) Найти производную по направлению биссектрисы первого координатного угла в т. М(1;1) функции 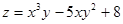
2) Найти градиент 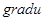 и
и 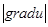 :
:
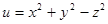 в точке М(1; -1; 2)
в точке М(1; -1; 2)
6. Написать уравнение касательной плоскости и нормали к поверхности:
1) 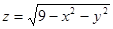 в точке М(1; 2; 2).
в точке М(1; 2; 2).
3) 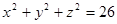 в точке М(3; 4; 1)
в точке М(3; 4; 1)
7. Найти экстремумы функций:
1) 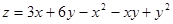
2) 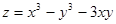
8. Вычислить двойные интегралы по указанным областям:
1) 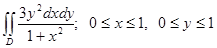
2) 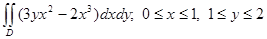
3) 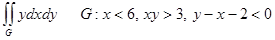
4) 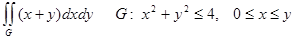
9. Вычислить длину дуги, заданной уравнением в прямоугольной системе координат: 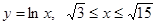 .
.
10.Вычислить длину дуги, заданной параметрически уравнениями:
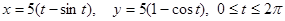 .
.
11. Вычислить длину дуги кривой, заданной в полярных координатах:
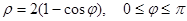
12. Исследовать сходимость знакоположительных рядов:
1) 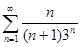 ; 2)
; 2) 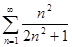 ; 3)
; 3) 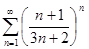 ; 4)
; 4) 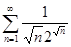
13. Исследовать функцию и построить график: 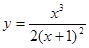
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|