Вариант 1 с пояснениями и ответами

Вариант 1 с пояснениями и ответами

Футболка стоила 360 рублей. После повышения цены она стала стоить 378 рублей. На сколько процентов была повышена цена на футболку?

Решение.

Цена на футболку была повышена на 378 −360 = 18 рублей. Поскольку

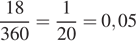цена на футболку была повышена на 5%.

Ответ: 5.

На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, на сколько градусов Цельсия март был в среднем холоднее августа.

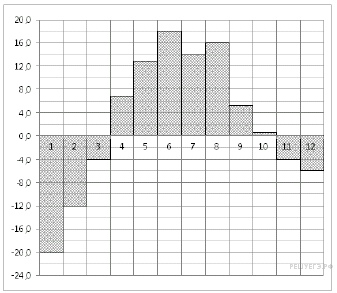
Решение.

Из диаграммы видно, что среднемесячная температура в марте равна −4 °C, а в августе — 16 °C. Следовательно, разность температур: 16 − (−4) = 20.

Ответ: 20.

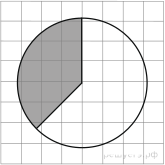На клетчатой бумаге с размером клетки 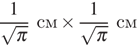изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.

Решение.

Найдем квадрат радиуса круга 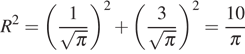см².

Площадь фигуры равна трем восьмым площади этого круга. Поэтому

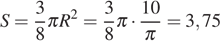см².

Ответ: 3,75.

Вероятность того, что новый электрический чайник прослужит больше года, равна 0,93. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

Решение.

Пусть A = «чайник прослужит больше года, но меньше двух лет», В = «чайник прослужит больше двух лет», С = «чайник прослужит ровно два года», тогда A + B + С = «чайник прослужит больше года».

События A, В и С несовместные, вероятность их суммы равна сумме вероятностей этих событий. Вероятность события С, состоящего в том, что чайник выйдет из строя ровно через два года — строго в тот же день, час и секунду — равна нулю. Тогда:

P(A + B+ С) = P(A) + P(B)+ P(С)= P(A) + P(B),

откуда, используя данные из условия, получаем

0,93 = P(A) + 0,87.

Тем самым, для искомой вероятности имеем:

P(A) = 0,93 − 0,87 = 0,06.

Ответ: 0,06.

Решите уравнение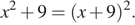

Решение.

Воспользуемся формулой :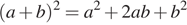

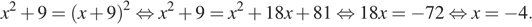
Ответ: −4.

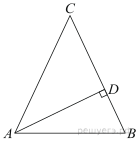В треугольнике ABC AC = BC, AD — высота, угол BAD равен 24°. Найдите угол C. Ответ дайте в градусах.

Решение.

Треугольник ABC равнобедренный, значит, углы при его основании равны.

Ответ: 48.

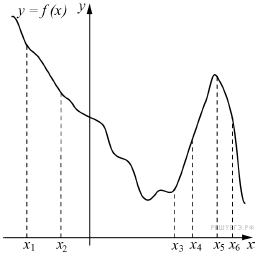
На рисунке изображён график функции y = f(x) и шесть точек на оси абсцисс: x₁, x₂, x₃, …, x₆. В скольких из этих точек производная функции f(x) положительна?

Решение.

Положительным значениям производной соответствует интервалы, на которых функция 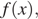возрастает. На них лежат точки Таких точек 2.

Ответ: 2.

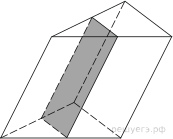Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объём этой призмы, если объём отсеченной треугольной призмы равен 5.

Решение.

Площадь основания отсеченной части меньше площади основания всей призмы в 4 раза (так как и высота и основание треугольника уменьшились в 2 раза). Высоты обеих частей призмы одинаковы, поэтому объем отсеченной части в 4 раза меньше объема целой призмы. Тем самым, он равен 20.

Ответ: 20.

Найдите значение выражения 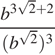при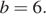

Решение.

Выполним преобразования:

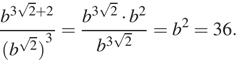
Ответ: 36.

От

10.

Уравнение процесса, в котором участвовал газ, записывается в виде 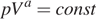, где p (Па) — давление в газе, V — объeм газа в кубических метрах, a — положительная константа. При каком наименьшем значении константы a уменьшение в 16 раз объeма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 2 раза?

Решение.

Пусть 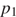и 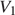– начальные, а 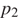и 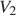– конечные значения объема и давления газа, соответственно. Условие 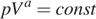означает, что откуда 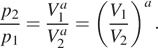Задача сводится к решению неравенства 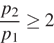, причем по условию :

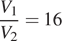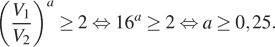
Ответ: 0,25.

11.

Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 12 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?

Решение.

Виноград содержит 10% питательного вещества, а изюм — 95%. Следовательно, 12 кг изюма содержат 12 · 0,95 = 11,4 кг питательного вещества. Таким образом, для получения 12 килограммов изюма требуется

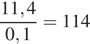
килограмм винограда.

Ответ: 114.

12.

Найдите наименьшее значение функции 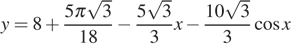на отрезке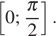

Решение.

Найдем производную заданной функции:

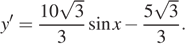
Найдем нули производной на заданном отрезке:

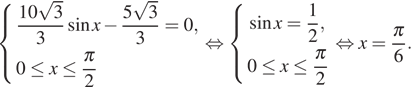
Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:

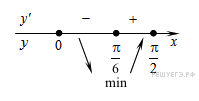
В точке 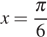заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:

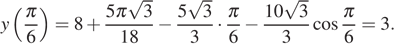
Ответ: 3.

13.

а) Решите уравнение .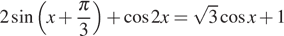

б) Определите, какие из его корней принадлежат отрезку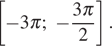

Решение.

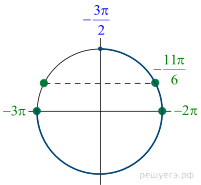а) Запишем исходное уравнение в виде:

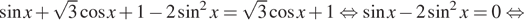
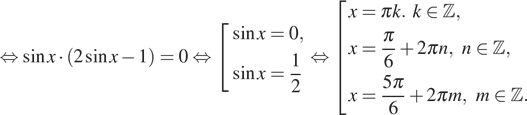
б) С помощью числовой окружности отберем корни, принадлежащие отрезку 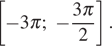Получим числа: .

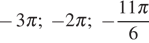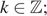
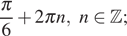
Ответ: а) 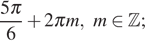б) .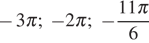

14.

Основание пирамиды PABC ― правильный треугольник ABC, сторона которого равна 16, боковое ребро PA ― 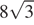. Высота пирамиды PH делит высоту AM треугольника ABC пополам. Через вершину A проведена плоскость, перпендикулярная прямой PM и пересекающая прямую PM в точке K.

а) Докажите, что плоскость делит высоту PH пирамиды PABC в отношении 2:1, считая от вершины P.

б) Найдите расстояние между прямыми PH и CK.

Решение.

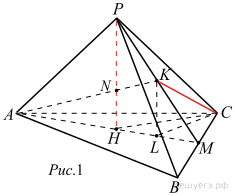
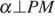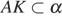а) Пусть прямая AK пересекает прямую PH в точке N (см. рисунок 1). Так как и , то 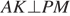. Далее имеем: 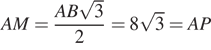. Значит, AK ― высота и медиана треугольника PAM. Следовательно, N ― точка пересечения медиан этого треугольника, откуда и получаем 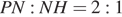, что и требовалось доказать.

б) Пусть точка L ― проекция точки K на плоскость ABC, тогда и, значит, 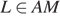. Так как и , то L ― середина MH. Отрезок CL ― проекция отрезка CK на плоскость ABC.

Далее, поскольку 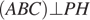, точка H ― проекция прямой PH на плоскость ABC. Значит, расстояние между прямыми PH и CK равно расстоянию от точки H до прямой CL, т.е., высоте HF треугольника CHL. (см. рисунок 2).

Далее имеем: , ,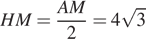

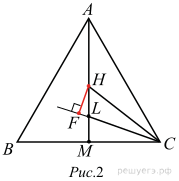
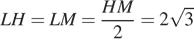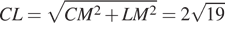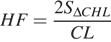, . Так как , то . Таким образом, .

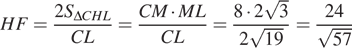Ответ: б) .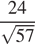

15. Задание

Решите неравенство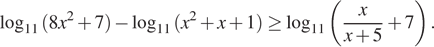

Решение.

Правая часть неравенства определена при или .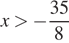

Поскольку при любых значениях x выражение 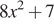принимает положительные значения, при или 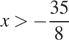неравенство принимает вид:

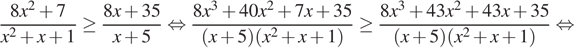
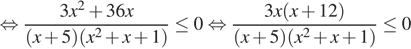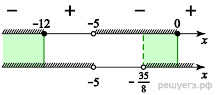
откуда . Учитывая, ограничения или 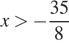, получаем: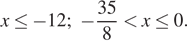

Ответ: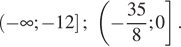

16.

Прямые, содержащие катеты AC и CB прямоугольного треугольника АСВ, являются общими внутренними касательными к окружностям радиусов 2 и 4. Прямая, содержащая гипотенузу АВ, является их общей внешней касательной.

а) Докажите, что длина отрезка внутренней касательной, проведенной из вершины острого угла треугольника до одной из окружностей, равна половине периметра треугольника АСВ.

б) Найдите площадь треугольника АСВ.

Решение.

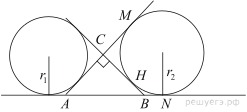а) Введём обозначения, как показано на рисунке, пусть M, H, N — точки касания. Касательные, проведённые к окружности из одной точки равны: AM = AN, CM = CH, HB = BN. Поэтому:

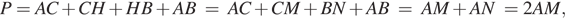
откуда p = AM.

б) Для определения площади треугольника используем формулу, связывающую её с полупериметром, стороной и радиусом вневписанной окружности, касающейся этой стороны и продолжений двух других сторон треугольника:

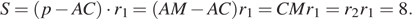
Ответ: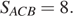

Примечание: указанная в решении формула легко может быть получена из следующих соображений 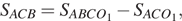где O₁ — центр окружности с радиусом r_1. При этом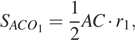

Тогда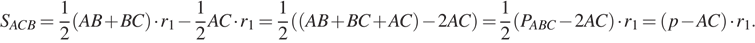

17.

Гражданин Петров по случаю рождения сына открыл 1 сентября 2008 года в банке счёт, на который он ежегодно кладет 1000 рублей. По условиям вклада банк ежегодно начисляет 20% на сумму, находящуюся на счёте. Через 6 лет у гражданина Петрова родилась дочь, и 1 сентября 2014 года он открыл в другом банке счёт, на который ежегодно кладёт по 2200 рублей, а банк начисляет 44% в год. В каком году после очередного пополнения суммы вкладов сравняются, если деньги со счетов не снимают?

Решение.

Через 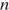лет 1 сентября на первом счёте будет сумма (суммируем n + 1 член геометрической прогрессии)

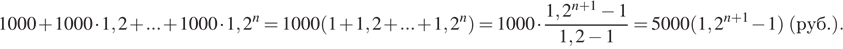
В это же время на втором счёте будет сумма

Приравняем эти суммы и решим полученное уравнение:

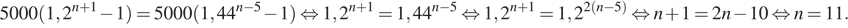
Таким образом, суммы на счетах сравняются через 11 лет после открытия первого вклада, то есть в 2019 году.

Ответ: 2019.

18.

Найдите все значения a, при которых уравнение

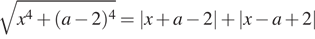
имеет единственное решение.

Решение.

Заметим, что если число x₀ является решением уравнения, то и число −x₀ также является решением этого уравнения. Значит, если уравнение имеет единственное решение, то это решение x = 0.

При x = 0 уравнение принимает вид

откуда a = 0, a = 2, a = 4.

При a = 0 и a = 4 исходное уравнение принимает вид 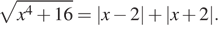При x < −2 правая часть уравнения 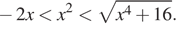При 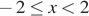левая часть уравнения не меньше 4, причём равенство достигается только при x = 0. При x > 2 правая часть уравнения Значит, исходное уравнение имеет единственное решение x = 0.

При a = 2 исходное уравнение принимает вид Числа −2, 0 и 2 являются корнями этого уравнения.

Таким образом, исходное уравнение имеет единственное решение при a = 0 и a = 4.

Ответ: 0; 4.

19.

В игре «Дротики» есть 20 наружных секторов, пронумерованных от 1 до 20 и два центральных сектора. При попадании в наружный сектор игрок получает количество очков, совпадающее с номером сектора, а за попадание в центральные сектора он получает 25 или 50 очков соответственно. В каждом из наружных секторов есть области удвоения и утроения, которые, соответственно, удваивают или утраивают номинал сектора. Так, например, попадание в сектор 10 (не в зоны удвоения и утроения) дает 10 очков, в зону удвоения сектора ― 20 очков, в зону утроения ― 30 очков.

а) Может ли игрок тремя бросками набрать ровно 161 очко?

б) Может ли игрок четырьмя бросками набрать ровно 235 очков?

в) С помощью какого наименьшего количества бросков, игрок может набрать ровно 947 очков?

Решение.

а) Да, например, при попадании в утроение сектора 20, утроение сектора 17 и центральный сектор 50 получаем: 60 + 51 + 50 = 161.

б) Наибольшее количество очков, которое может набрать игрок одним броском ― 60 (утроение 20), далее идут: 57 очков (утроение 19) и 54 очка (утроение 18). Попадание во все остальные сектора и зоны дают меньше 54 очков. Если все четыре броска были по 60 очков, то игрок набрал 240 очков, что больше 235. Если хотя бы один бросок на 60 очков заменить броском на 54 очка или меньше, то сумма уменьшится как минимум на 6, а, значит, станет не больше 234 очков, что меньше 235 очков. Следовательно, бросок на 60 очков можно заменять только броском на 57 очков. Но одна такая замена дает итоговый результат 237 очков, а хотя бы две замены ― не более 234 очков. Значит, 235 очков четырьмя бросками набрать невозможно.

в) Как было показано в пункте б) каждый бросок приносит игроку не более 60 очков. Значит, за 15 бросков он наберет не более 900 очков, а тогда для того, чтобы набрать 947 очков понадобится не менее 16 бросков.

Покажем, что игрок может набрать 947 очков за 16 бросков. Предположим, что он сделал 14 бросков на 60 очков (итого 840), один бросок в зону утроения сектора 19 (57 очко) и один бросок в центральный сектор 50 очков. Тогда в сумме он наберет 840 + 57 + 50 = 947 очков.

Отметим, что в пунктах а) и в) учащийся мог привести другие верные примеры.

Ответ: а) да; б) нет; в) за 16 бросков.