
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
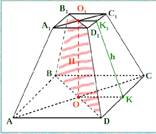
Усеченная пирамида
Усеченная пирамида
Усеченная пирамида это часть пирамиды, заключенная между ее основанием и секущей плоскостью, параллельной основанию.
Основание и соответствующее сечение усеченной пирамиды называются основаниями усеченной пирамиды.
Основания усеченной пирамиды являются подобными многоугольниками, их стороны попарно параллельны, боковые грани усеченной пирамиды трапеции.
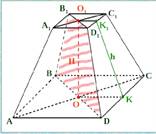 АВСД – нижнее основание, А1В1С1Д1- верхнее основание.
АВСД – нижнее основание, А1В1С1Д1- верхнее основание.
ОО1=H – перпендикуляр проведенный из какой либо точки одного основания на плоскость другого.
ВВ1Д1Д- диагональное сечение ( проходит через два боковые ребра
не лежащие в одной грани.
Правильная усеченная пирамида часть правильной полной пирамиды, основания будут правильные многоугольники (квадраты).
КК1= a - апофема, высота боковой грани правильной усеченной пирамиды.
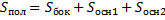
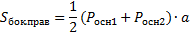
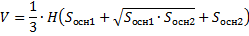
Типовая задача №1
 В правильной четырехугольной усеченной пирамиде стороны оснований 6 и 16 м, высота 12 м. Найти полную поверхность.
В правильной четырехугольной усеченной пирамиде стороны оснований 6 и 16 м, высота 12 м. Найти полную поверхность.
Дано: АВСДА1В1С1Д1- правильная усеченная пирамида.
АВ=16м, А1В1=6м, ОО1=12м.
Найти: Sпол-?
Решение
1. 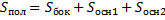 т.к усеченная пирамида правильная, в основаниях лежат квадраты, найдем площадь оснований
т.к усеченная пирамида правильная, в основаниях лежат квадраты, найдем площадь оснований
2. 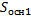 =АД2=162=256 м2
=АД2=162=256 м2
3. 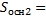 А1В12=62=36 м2
А1В12=62=36 м2
4. 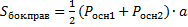
5. 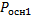 =4*АВ=4*16=64 м
=4*АВ=4*16=64 м
6.  =4*А1В1=4*6=24 м
=4*А1В1=4*6=24 м
7. 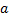 =КК1– апофему найдем из прямой трапеции ОО1К1К т.к в основаниях лежат квадраты ,то точка О и О1 центры вписанных и описанных окружностей, ОК и О1К1 – это радиусы вписанных окружностей ( смотрим справочный материал
=КК1– апофему найдем из прямой трапеции ОО1К1К т.к в основаниях лежат квадраты ,то точка О и О1 центры вписанных и описанных окружностей, ОК и О1К1 – это радиусы вписанных окружностей ( смотрим справочный материал 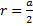 ,где a- сторона квадрата)
,где a- сторона квадрата) 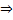 ОК=r1, О1К1= r2
ОК=r1, О1К1= r2
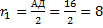 м
м

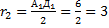 м
м
Проведем из вершины К1 перпендикуляр К1Н к нижнему основанию прямой трапеции ОО1К1К, рассмотрим 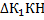 – прямоугольный по построению, т.к
– прямоугольный по построению, т.к 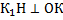 , К1Н=ОО1=12 м, НК= ОК- О1К1= 8-3=5 м.
, К1Н=ОО1=12 м, НК= ОК- О1К1= 8-3=5 м.
По теореме Пифагора 
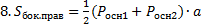 =
= 
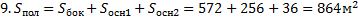
Ответ: 864 м2полная поверхность усеченной пирамиды.
Типовая задача №2
В правильной треугольной усеченной пирамиде стороны основания  и
и 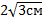 , апофема равна 6 см. Найти объем пирамиды
, апофема равна 6 см. Найти объем пирамиды

Дано: АВСА1В1С1- правильная усеченная пирамида, АВ=  , А1В1=
, А1В1= 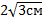 , М1М- апофема=6см.
, М1М- апофема=6см.
Найти V-?
Решение.
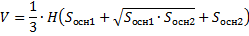
1. Т.к усеченная пирамида правильная и треугольная, то в основаниях лежат равносторонние треугольники. Найдем площади оснований
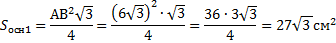
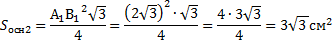
2. h= OO1- ? найдем из прямой трапеции ОО1М1М.
3. т.к в основаниях лежат равносторонние треугольники ,то точка О и О1 центры вписанных и описанных окружностей, ОМ и О1М1 – это радиусы вписанных окружностей ( смотрим справочный материал 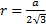 ,где a- сторона квадрата)
,где a- сторона квадрата) 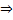 ОМ=r1, О1М1= r2
ОМ=r1, О1М1= r2
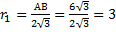 см
см
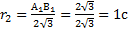 м
м

4. Проведем из вершины М1 перпендикуляр М1Н к нижнему основанию прямой трапеции ОО1М1М, рассмотрим 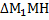 – прямоугольный по построению, т.к
– прямоугольный по построению, т.к 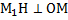 , М1Н=ОО1, НМ= ОМ- О1М1= 3-1=2см. По теореме Пифагора найдем М1Н.
, М1Н=ОО1, НМ= ОМ- О1М1= 3-1=2см. По теореме Пифагора найдем М1Н.
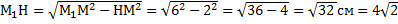 см , т.к М1Н= ОО1
см , т.к М1Н= ОО1 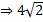 см
см
5. 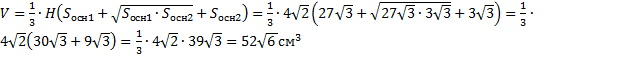
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|