
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ДИСТАНЦИОННОЕ ОБУЧЕНИЕ. Урок Простейшие показательные уравнения.. Повторить. Простейшие показательные уравнения- это уравнения, где неизвестное находится в показатели степени .. Привести обе части равенства к одному основанию. Если степени равны, основани
ДИСТАНЦИОННОЕ ОБУЧЕНИЕ
Урок Простейшие показательные уравнения.
Цели: формирование навыков решения простейших показательных уравнений; решение показательных уравнений.
Повторить
1. Определение степени с целым показателем
2. Свойства степеней
Простейшие показательные уравнения- это уравнения, где неизвестное находится в показатели степени .
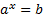
При решении показательных уравнений используется понятие степени и свойства степени:
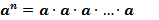 n раз
n раз 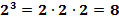
а - основание степени, n – показатель степени
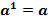 любое число можно представить в виде степени с показателем 1
любое число можно представить в виде степени с показателем 1
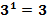 ,
, 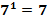 и наоборот 2=
и наоборот 2= 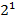 , 9=
, 9= 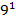
Свойства степеней:
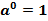
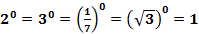
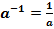
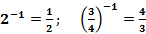 и наоборот
и наоборот 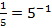
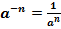
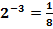 и наоборот
и наоборот 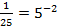 ,
, 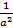 =
= 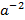
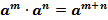
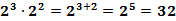 ;
; 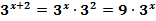
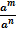 =
= 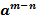
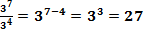 ;
; 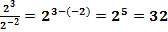 ;
;
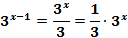
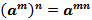
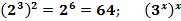 =
= 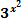
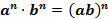
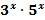 =
= 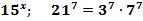
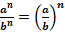
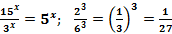
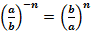
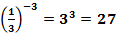
Алгоритм решения простейших показательных уравнений:
1. Привести обе части равенства к одному основанию
2. Если степени равны, основания степеней равны, то и показатели равны
3. Приравнять показатели и решить получившееся уравнение.
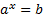
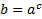
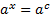
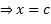
Пример 1. Решить уравнение 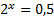
Решение. Приведем обе части равенства к одному основанию: 0,5= 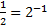
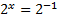
Так как значения степеней равны, основания равны, то и показатели степеней равны, получим уравнение: x= -1.
Ответ: -1.
Пример 2. Решить уравнение 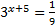 .
.
Решение. Приведем обе части равенства к одному основанию: 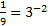
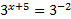
Так как значения степеней равны, основания равны, то и показатели степеней равны, получим уравнение: x+5= -2
x= -2-5
x=-7
Ответ: -7.
Пример 3. Решить уравнение 0,04 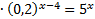
Решение. Приведем обе части равенства к основанию 5, используя свойства степеней:
0,2= 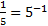 ; 0,04=
; 0,04= 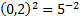 ,
,
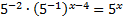
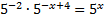 по свойству
по свойству 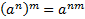
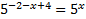 по свойству
по свойству 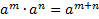
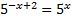
Так как значения степеней равны, основания равны, то и показатели степеней равны, получим уравнение: - x+2= x
-x-x= -2
-2x= -2
x= 1.
Ответ: 1.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|