
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ДИСТАНЦИОННОЕ ОБУЧЕНЕ. Урок Практическая работа «Простейшие тригонометрические уравнения». Арккосинусом числа а , , называется такое число , косинус которого равен а.. Арксинусом числа а , , называется такое число , синус которого равен а.. Арктангенсом
ДИСТАНЦИОННОЕ ОБУЧЕНЕ
Урок Практическая работа «Простейшие тригонометрические уравнения»
Цели: изучить понятиеарксинуса, арккосинуса, арктангенса, научиться находить их значения и решать с их помощью простейшие тригонометрические уравнения .
Тригонометрические уравнения. Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическим.
Цели:.
Тригонометрические уравнения вида:
1. Sin x=a 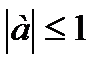
2. Cos x=a 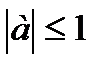

3. tg x=a
4. Ctg x=a имеют корни уравнения, которые называются соответственно арккосинус, арксинус, арктангенс и арккотангенс соответственно.
1. Арккосинусом числа а , , называется такое число , косинус которого равен а.
Обозначаются arccos a= 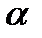 , cos
, cos 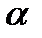 =a,
=a, 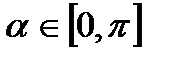 .
.
Например, arccos  , т.к. cos
, т.к. cos 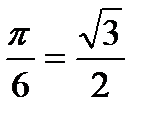
При  Решением уравнения Cos х=а является
Решением уравнения Cos х=а является 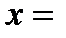
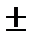
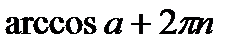 ,
, 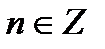
При  Решением уравнения Cos x=a является
Решением уравнения Cos x=a является 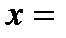
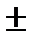
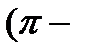
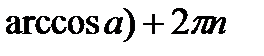 ,
, 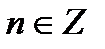
2. Арксинусом числа а , , называется такое число , синус которого равен а.
Обозначается arcsin a= 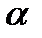 , sin
, sin 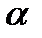 =a,
=a,  .
.
Например, arcsin 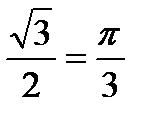 , т.к. sin
, т.к. sin 
При  Решением уравнения sin x=a является
Решением уравнения sin x=a является
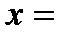
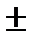
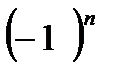
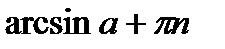 ,
, 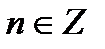
При  Решением уравнения sin x=a является
Решением уравнения sin x=a является
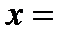
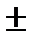 (
( 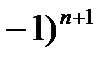
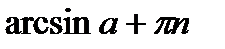 ,
, 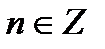
3. Арктангенсом числа а , , называется такое число , тангенс которого равен а.
Обозначается arctg a= 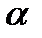 , tg
, tg 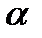 = a,
= a,  .
.
Если 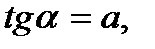 то
то 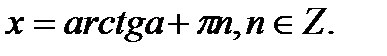
Простейшие тригонометрические уравнения:


Уравнения, содержащие тангенс и котангенс
tg x = a
x = arctg a + pk, k Î Z
ctg x = a
x = arcctg a + pk, k Î Z
Частные случаи:
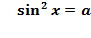 ,
, 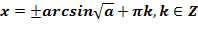
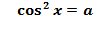 ,
, 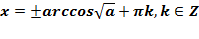
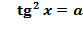 ,
, 
Решить уравнения:
1. Sin 2x=-1
2. Sin ( 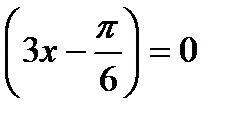
3. 3cos7x=-3
4. Cos 
5. cos 
6. cos 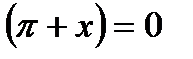
7. 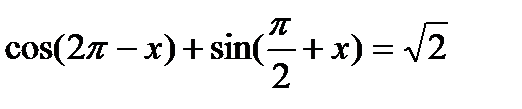
8. 
9. 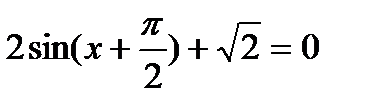
10. 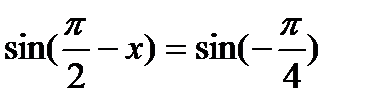
Решить задачи: №656,657, 659.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|