
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ДИСТАНЦИОННОЕ ОБУЧЕНИЕ. Урок Определенный интеграл. Формула Ньютона-Лейбница.. Изучение нового: Параграф 56.. Определенный интеграл. Основные понятия и определения. Формула Ньютона- Лейбница.. Вычислить определённый интеграл.
ДИСТАНЦИОННОЕ ОБУЧЕНИЕ
Урок Определенный интеграл. Формула Ньютона-Лейбница.
Цели: Повторить знания о первообразной.
 Закрепить навыки нахождения табличных интегралов, площадей криволинейных трапеций с помощью формулы Ньютона-Лейбница.
Закрепить навыки нахождения табличных интегралов, площадей криволинейных трапеций с помощью формулы Ньютона-Лейбница.
 Проверить уровень сформированности навыка нахождения первообразных.
Проверить уровень сформированности навыка нахождения первообразных.
 Способствовать выработке вычислительных навыков.
Способствовать выработке вычислительных навыков.
 Развивать логическое мышление, память, внимание и самостоятельность.
Развивать логическое мышление, память, внимание и самостоятельность.
Изучение нового: Параграф 56.
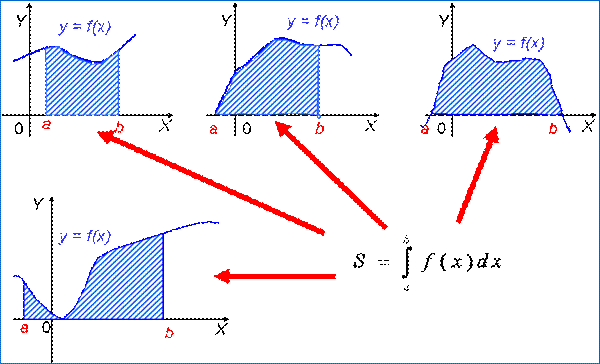
Определенный интеграл. Основные понятия и определения
Криволинейная трапеция – плоская фигура, ограниченная графиком функции 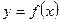 , отрезками прямыхx=a, x=b и осью Ox.
, отрезками прямыхx=a, x=b и осью Ox.
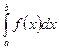 называется определенным интегралом функции
называется определенным интегралом функции 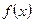 на отрезке
на отрезке 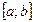
Замечание. С геометрической точки зрения при 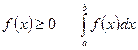 равен площади криволинейной трапеции.
равен площади криволинейной трапеции.
Формула Ньютона- Лейбница.
Теорема. Пусть 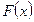 - первообразная функции
- первообразная функции 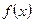 . Тогда
. Тогда
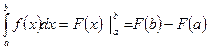
|
Эта формула называется формулой Ньютона – Лейбница, из нее следует, что для вычисления определенного интеграла необходимо найти первообразную подынтегральной функции.
Вычислить определённый интеграл.
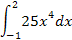 1.1 1.1
| 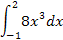 1.6 1.6
| 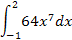 1.11 1.11
|
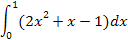 1.2 1.2
| 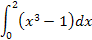 1.7 1.7
| 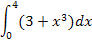 1.12 1.12
|
 1.3 1.3
| 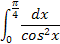 1.8 1.8
| 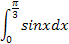 1.13 1.13
|
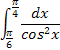 1.4 1.4
|  1.9 1.9
| 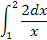 1.14 1.14
|
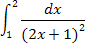 1.5 1.5
| 1.10 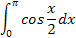
| 1.15 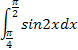
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|