Тема № 4 . ИНФОРМАЦИОННЫЕ ПРОЦЕССЫ

Учебная дисциплина: ОДП.04. Информатика и ИКТ.

Группа: АМ-2-19.

Профессия: 23.01.03.Автомеханик

Дата проведения: 15.06.20 г.

Тема № 4 . ИНФОРМАЦИОННЫЕ ПРОЦЕССЫ

Урок № 41

ПРАКТИЧЕСКАЯ РАБОТА № 3.

ТЕМА: ПРОГРАММИРОВАНИЕ МОДЕЛИ РАБОТЫ АЛГОРИТМА ХЕММИНГА.

Цель работы:обобщить знания по программированию модели работы алгоритма Хемминга.

Практическая работа состоит из двух частей. Сегодня выполняем первую часть работы.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ.

Коды Хэмминга — наиболее известные и, вероятно, первые из самоконтролирующихся и самокорректирующихся кодов. Построены они применительно к двоичной системе счисления.

Другими словами, это алгоритм, который позволяет закодировать какое-либо информационное сообщение определённым образом и после передачи (например по сети) определить появилась ли какая-то ошибка в этом сообщении (к примеру из-за помех) и, при возможности, восстановить это сообщение. Сегодня, я опишу самый простой алгоритм Хемминга, который может исправлять лишь одну ошибку.

Также стоит отметить, что существуют более совершенные модификации данного алгоритма, которые позволяют обнаруживать (и если возможно исправлять) большее количество ошибок.

Сразу стоит сказать, что Код Хэмминга состоит из двух частей. Первая часть кодирует исходное сообщение, вставляя в него в определённых местах контрольные биты (вычисленные особым образом). Вторая часть получает входящее сообщение и заново вычисляет контрольные биты (по тому же алгоритму, что и первая часть). Если все вновь вычисленные контрольные биты совпадают с полученными, то сообщение получено без ошибок. В противном случае, выводится сообщение об ошибке и при возможности ошибка исправляется.

Минимальное количество символов, в которых все кодовые комбинации отличаются друг от друга, называется кодовым расстоянием.

Для исправления одной ошибки кодовое расстояние должно быть не менее 3 ( ).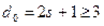

Для того чтобы в принятом сообщении можно было исправлять ошибки, кодовая комбинация должна обладать некоторой избыточностью, которая достигается за счет добавления контрольных разрядов. Число корректирующих разрядов должно удовлетворять следующим условиям.

Пусть r – число корректирующих символов, k – количество информационных разрядов, n– длина кода, тогда

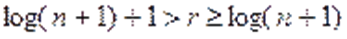
Код Хемминга является типичным примером систематического кода и может строиться на основе производящей матрицы. Порождающая матрица имеет k строк и n столбцов.

Порождающая матрица G может быть представлена двумя матрицами, единичной и добавочной. При выборе добавочной матрицы учитывают, что вес (весом двоичного вектора называется величина расстояния Хемминга от него до нулевого вектора) каждой строки не должен быть менее .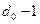

Кодирование реализуется при помощи умножения информационной комбинации α на порождающую матрицу

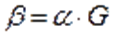
Проверочная матрица Н при двоичном кодировании представляет собой транспонированную добавочную матрицу, дополненную единичной. Проверочная матрица имеет r строк и n столбцов. Причем столбцы представляют собой значения синдрома для разряда, соответствующего номеру этого столбца.

Для определения синдрома необходимо умножить кодовую комбинацию на транспонированную проверочную матрицу

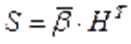
ПРИМЕР

ЗАДАНИЕ. Методом Хемминга закодировать комбинацию α=1101, построив порождающую проверочную матрицы. Внести ошибку в один из разрядов кодового вектора; найти синдром; найти и исправить ошибку.

Нетрудно видеть, что число информационных разрядов k=4, определим r, n.

Для расчета r можем использовать эмпирическую формулу

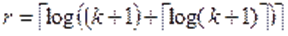Получим r=3, n=7.

Имеем (7,4)– кодирование. Порождающая матрица G имеет размерность 4×7, а проверочная – 3×7.

Построим проверочную матрицу Н, так чтобы ее столбцы были различны и не содержали нулевую комбинацию:

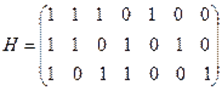, d₀≥3

Строим порождающую матрицу G:

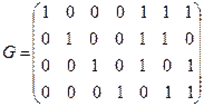
Кодовая комбинация β имеет вид β=αG=1101010,

Внесем ошибку в третий разряд 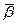=1111010, вычислим синдром 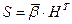=101,что соответствует ошибке в третьем разряде. Исправленная кодовая комбинация β_исп =1101010.

ДОМАШНЕЕ ЗАДАНИЕ:

1. Методом Хемминга закодировать указанные информационные комбинации, построив порождающую проверочную матрицы. Внести ошибку в один из разрядов кодового вектора; найти синдром; найти и исправить ошибку.

2.Ответить на вопросы:

2.1. Линейное кодирование. Основные понятия.

2.2. Порождающая и проверочная матрицы; синдром.

2.3. Помехоустойчивое кодирование. Основные понятия. Расстояние Хемминга; кодовое расстояние.

2.4. Метод кодирования Хемминга.

Ответы на домашнее задание выслать (в виде фотографий или документов Microsoft Word) на электронный адрес:

larisanikolaevna.epgl@yandex.ru