Решить самостоятельно

Векторы в пространстве Ссылка на видеоурок https://infourok.ru/videouroki/1467

Задача. Вычислить угол между векторами 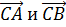, если известны координаты точек: А (1; 3; 0), B (2; 3; -1) и C(1; 2; -1).

Решение.1). Найдём координаты векторов 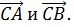(Из координат конца вектора вычитаем координаты начала вектора)

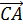= {1-1; 3 -2; 0-(-1)}= {0;1;1}

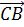={2-1; 3-2;-1-(-1)}= {1;1;0}

2). Найдём скалярное произведение векторов, оно равно сумме произведений соответствующих координат

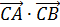= 0∙1 + 1∙1 + 1∙0=0+1+0=1

3). Найдём модуль (длину) каждого вектора (модуль вектора равен корню квадратному из суммы квадратов его координат)

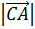²= 0²+1²+1²= 0+1+1=2 =

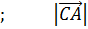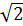
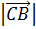²= 1²+1²+0²= 1+1+0=2 =

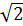
4)Найдём косинус угла между векторами (для этого надо скалярное произведение векторов разделить на произведение их модулей)

cos α= = =

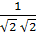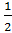
5)Получили, что cosα= 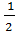⇒ α=60⁰. Ответ: 60⁰

Решить самостоятельно

Вычислить угол между векторами 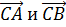, если известны координаты точек: А (1; 3; 0), B (2; 3; -1) и C(1; 2; -1). /Ответ: 120⁰/