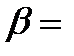- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Векторы в пространстве. Метод координат в пространстве
Векторы в пространстве
Данное пособие включает в себя перечень основных формул на применение координат и векторов при вычислении расстояний, углов, площадей и объёмов в стереометрических задачах. Затем приводятся примеры решения задач различного уровня сложности и упражнения для самостоятельного решения (с ответами)
Рекомендации по работе с пособием:
1. Внимательно ознакомьтесь со справочным материалом, при необходимости повторите теоретический материал по школьному учебнику или по другим источникам (см. список литературы). Применение основных формул сопровождается иллюстрирующими задачами.
2. Прочитав задачу, попытайтесь решить её самостоятельно, не заглядывая в решение, предложенное в пособии. Не исключено, что Ваше решение может оказаться более рациональным или оригинальным.
3. Если же задачу не удаётся решить самостоятельно, посмотрите начало решения, указанное в пособии. Возможно, Вам достаточно будет какой-то начальной идеи, чтобы завершить решение самостоятельно.
4. Если всё-таки задачу решить не можете, ознакомьтесь с полным решением, предложенным в пособии. После этого обязательно перерешайте разобранную задачу от начала до конца самостоятельно.
5. В некоторых задачах предложены несколько способов решения. Разберите каждый! После этого переходите к упражнениям для самостоятельной работы.
Метод координат в пространстве
| Прямые x,y,z называются координатными осями (или осями координат), Оси координат обозначаются так: OX- ось абсцисс OY- ось ординат OZ- ось аппликат точка их пересечения O – началом координат, а плоскости xOy, xOz и yOz – координатными плоскостями. В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел, которые называются ее координатами. М(x; y; z). |
Прямоугольная система координат в пространстве
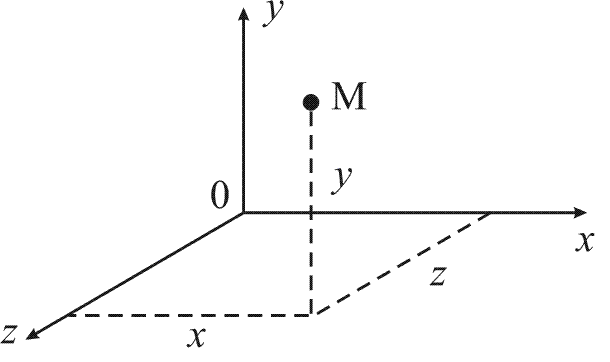
|
| Действия над векторами: |
Сложение векторов
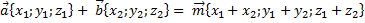
|
Вычитание векторов
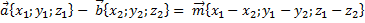
|
Умножение вектора на число k.

|
Координаты середины отрезка AB:
А(x1;y1;z1), B(x2;y2;z2).
Точка М середина отрезка AB.
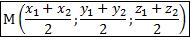
|
Вычисление длины вектора 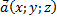 по его координатам: по его координатам:
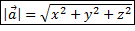
|
Расстояние между двумя точками.
А(x1;y1;z1) и B(x2;y2;z2).
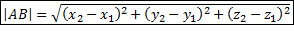
|
Вычисление координат вектора 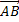 . Если А(x1;y1;z1), B(x2;y2;z2). . Если А(x1;y1;z1), B(x2;y2;z2).
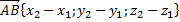
|
Скалярное произведение векторов 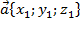 и и 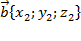 выражается формулой: выражается формулой:
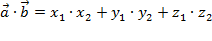
|
Перпендикулярность векторов: 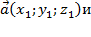 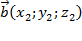 ; ;
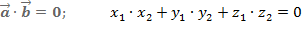
|
Коллинеарность векторов: 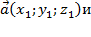 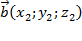 ; ;
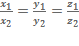 ,если координаты векторов не равны нулю. ,если координаты векторов не равны нулю.
|
Косинус угла между ненулевыми векторами векторов 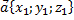 и и 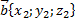 вычисляется по формуле: вычисляется по формуле:
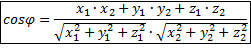
|
Задачи по теме «Векторы в пространстве»
1.Даны координаты точек А(-3; 2; -1), В(2; -1;-3), С(1; -4; 3), Д(-1; 2; -2).
Найдите | 2АВ+3СД |
Решение:
 (2+3; -1-2;-3+1)=(5;-3;-2)
(2+3; -1-2;-3+1)=(5;-3;-2)
 (-1-1;2+4;-2-3)=(-2;6;-5).
(-1-1;2+4;-2-3)=(-2;6;-5).
2 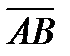 +3
+3 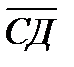 =(10+(-6);-6+18;-4-15)=(4;12;-19).
=(10+(-6);-6+18;-4-15)=(4;12;-19).

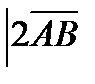 +3
+3 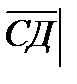 =
= 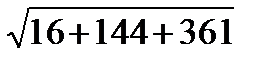 =
= 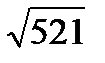
Ответ: 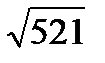
2. Даны координаты точек С(3; -2; 1), Д(-1; 2; 1), М(2; -3;3), N(-1; 1; -2). Найдите косинус угла между векторами 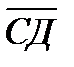 и
и 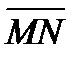 .
.
Решение:
cosα= 

CД(-4;4;0) 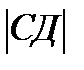 =
= 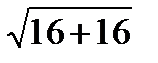 =4
=4 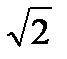
MN=(-3;4;-5) 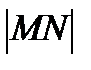 =
= 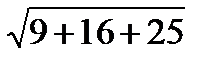 =5
=5 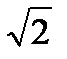
Cosα= 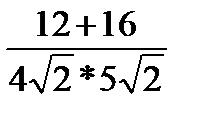 =
= 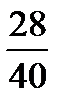 =0,7
=0,7
Ответ:0,7
3. Вычислите угол между векторами 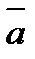 (2; -2; 0) и
(2; -2; 0) и 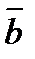 (3; 0; -3).
(3; 0; -3).
Решение:
Cos 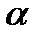 =
= 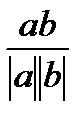
ab=2*3+(-2)*0+(-3)*0=6
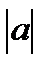 =
= 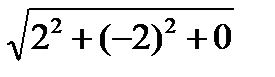 =2
=2 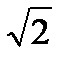
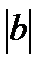 =
= 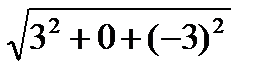 =3
=3 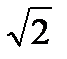
cos 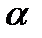 =
= 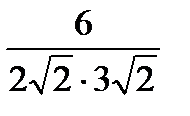 =
= 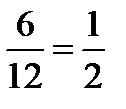
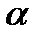 =600
=600
Ответ :600
4. При каком значении n данные векторы перпендикулярны: 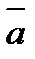 (2; -1;3) и
(2; -1;3) и 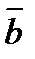 (1;3; n)?
(1;3; n)?
Решение:
ab=2*1-3*(-1)+3n
3n-1=0
3n=1
n= 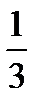
Ответ: 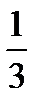
5.Вычислите координаты вектора 2 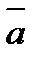 +3
+3 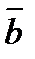 +
+ 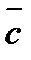 по координатам векторов:
по координатам векторов: 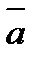 (3;1; 1),
(3;1; 1), 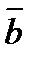 (-2;0;2)
(-2;0;2)
Решение:
2 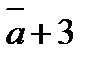
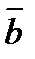 +
+ 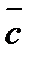 =(2*3;2*1;2*1)+(3*(-2);3*0;3*2)+(1;-1;0)=(6-6+1;2+0-1;2+6)=(1;1;8)
=(2*3;2*1;2*1)+(3*(-2);3*0;3*2)+(1;-1;0)=(6-6+1;2+0-1;2+6)=(1;1;8)
Ответ:(1;1;8)
6.Вычислите значение k , при котором скалярное произведение векторов 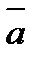 (2;k;-1) и
(2;k;-1) и
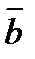 (3; -1; 2k) равно(-5)
(3; -1; 2k) равно(-5)
Решение:
ab=2*3-k-2k
6-k-2k=0
-3k=-11
k= 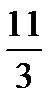
Ответ: 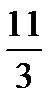
7.Даны векторы: 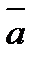 (-3;-1;2),
(-3;-1;2), 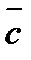 (5;-2;7). Найдите координаты вектора: -
(5;-2;7). Найдите координаты вектора: - 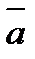 +3
+3 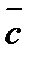 .
.
Решение:
- 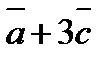 =(3;1;-2)+(3*5+3*(-2)+3*7)=(18;-5;-19)
=(3;1;-2)+(3*5+3*(-2)+3*7)=(18;-5;-19)
Ответ:(18;-5;-19)
8.При каких значениях x и у векторы а(х;-2;5) и b(1;у;-3) коллинеарные?
Решение:
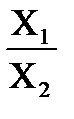 =
= 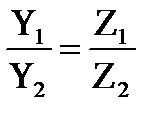 - свойство коллинеарных векторов
- свойство коллинеарных векторов
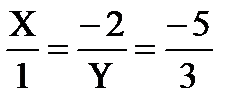
 -5
-5  =-6
=-6 
 =
= 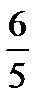
3х=-5 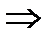 x=
x= 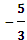
Ответ:x= 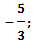
 =
= 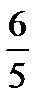
9.Вычислите длину вектора 2 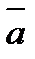 + 3
+ 3 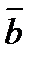 , если
, если 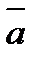 (3; 1;0),
(3; 1;0), 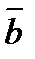 (0;1;-1).
(0;1;-1).
Решение:
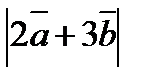
 =4a
=4a 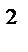 +12ab+9b
+12ab+9b 
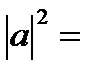 9+1=10
9+1=10
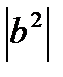 =1+1=2
=1+1=2
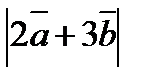
 =4*10+12+9*2=40+30=70
=4*10+12+9*2=40+30=70
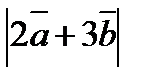 =
= 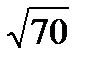
Ответ: 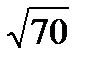
10.Даны две точки А(2;-1;3), В(1;0;4) и вектор 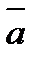 (4;-2;-3). Найдите длину вектора 3
(4;-2;-3). Найдите длину вектора 3 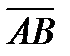 + 5
+ 5 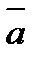
Решение:
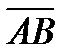 (1-2;0+1;4-3)=(-1;1;1) 3
(1-2;0+1;4-3)=(-1;1;1) 3 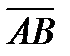 (-3;3;3)
(-3;3;3)
5 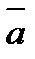 (20;-10;-15)
(20;-10;-15)
3 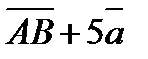 =(17;-7;-12)
=(17;-7;-12)
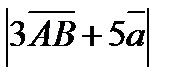 =
= 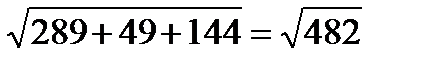
Ответ: 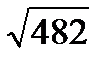
11.Даны точки А(2;0;1), В(4;-1;3), С(1;1;2). Найдите косинус внутреннего угла при вершине В треугольника АВС.
Решение:
cos 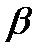 =
= 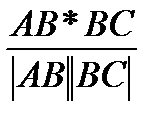
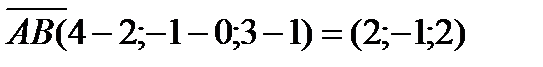
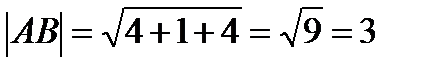

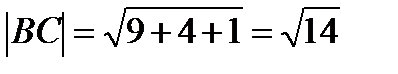
AB*BC=-3*2+(-1)*2+2(-1)=-6-2-2=-10
cos 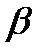 =
= 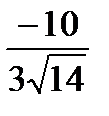 =
= 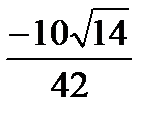 =
= 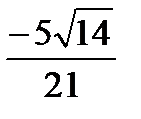
Ответ: 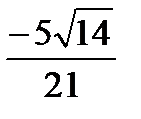
12.Найдите сумму всех значений m, при которых векторы а(m + 1; 1;-1;) и b(m; -m;-2m+3) перпендикулярны.
Решение:
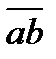 =0
=0
m(m+1)-m+2m-3=0
m 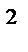 +2m-3=0
+2m-3=0
m 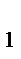 =-3
=-3
m 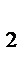 =1
=1
m 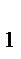 +m
+m 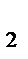 =-3+1=-2
=-3+1=-2
Ответ:-2
13.Найдите длину большей диагонали параллелограмма, построенного на векторах 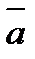 (3;-3;-2) и
(3;-3;-2) и 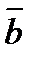 (1;2;-1).
(1;2;-1).
Решение:
d 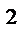 =(a+
=(a+ 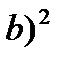

d 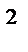 =a
=a 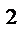 +2ab+b
+2ab+b 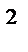
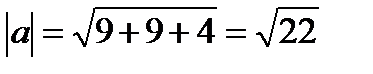
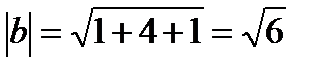
d 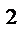 =22-2+6=26 ab=3-6+2=-1
=22-2+6=26 ab=3-6+2=-1
d= 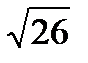
Ответ: 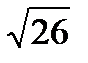
14.Найдите в градусах угол между векторами 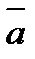 (1;1;
(1;1; 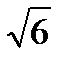 ) и осью Оz.
) и осью Оz.
Решение:
cos 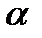 =
= 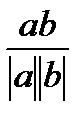
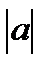 =
= 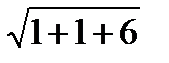 =
= 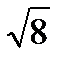

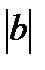 =
= 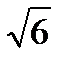
ab=0+0+6=6
cos 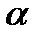 =
= 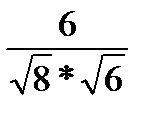 =
= 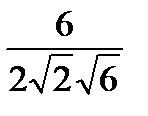 =
= 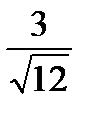 =
= 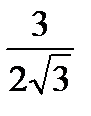 =
= 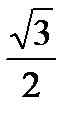
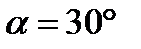
Ответ: 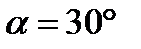
15.Даны векторы 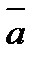 (-1;1;1;)
(-1;1;1;) 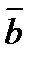 (0;2;-2). Найдите координаты вектора с
(0;2;-2). Найдите координаты вектора с 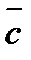 =(2
=(2 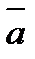 +3
+3 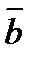 )-(
)-(  -2)
-2)  +2(
+2(  -
-  ).
).
Решение:
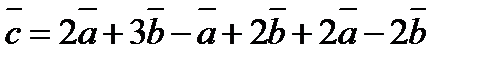 =3
=3 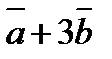
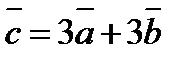 =(-3;3;3)+(0;6;-6)=(-3+0;3+6;3-6)=(-3;9;-3)
=(-3;3;3)+(0;6;-6)=(-3+0;3+6;3-6)=(-3;9;-3)
 (-3;9;-3)
(-3;9;-3)
Ответ:  (-3;9;-3)
(-3;9;-3)
16.Найдите значения m и n, при которых следующие векторы коллинеарные:  (15;m;1) и
(15;m;1) и  (18;12;n)
(18;12;n)
Решение:
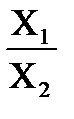 =
= 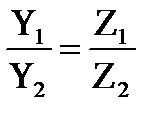 - свойство коллинеарных векторов
- свойство коллинеарных векторов
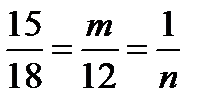
18m=180 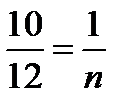
m=10 10n=12
n=1,2
Ответ:m=10,n=1,2
17.Даны векторы  =mi+3j+4k и
=mi+3j+4k и  =(4i+mj-7k). При каком значении векторы ортогональны?
=(4i+mj-7k). При каком значении векторы ортогональны?
Решение:
a(m;3;4) b(4;m;-7)
ab=0
4m+3m-28=0
7m=28
m=4
Ответ:4
18. Даны векторы  (-1;2;3) и
(-1;2;3) и  (5;х;-1). При каком значении х выполняется условие аb=3?
(5;х;-1). При каком значении х выполняется условие аb=3?
Решение:
ab=3
-5+2x-3=3
2x=6+5
x=5,5
Ответ:5,5
19.Вершины треугольника АВС имеют координаты А(-2;0;1), В(-1;2;3) и С(8;-4;9). Найдите координаты вектора ВМ, если ВМ медиана треугольника АВС.
Решение:
Точка М середина отрезка АС. 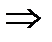 М(
М( 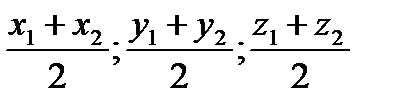 )
)
х  =
= 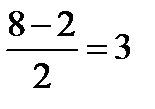 у
у 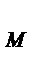 =
= 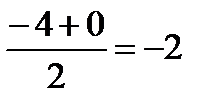 z
z 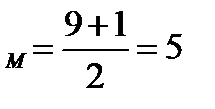 M(3;-2;5)
M(3;-2;5)
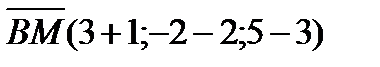
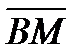 (4;-4;2)
(4;-4;2)
Ответ: 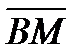 (4;-4;2)
(4;-4;2)
20.Даны вершины треугольника: А(-1;-2;4), В(-4;-2;0) и С(3;-2;1). Найдите угол треугольника при вершине А.
Решение:
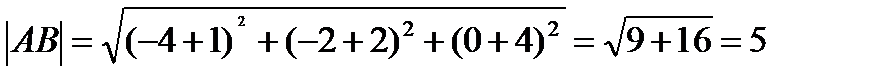
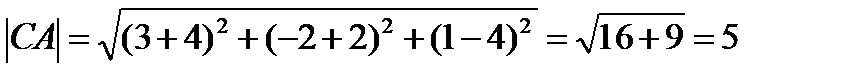
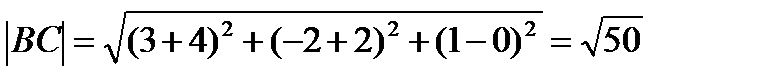 =2
=2 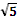
По теореме Пифагора  АВС прямоугольный ,равнобедренныйтреугольник значит,
АВС прямоугольный ,равнобедренныйтреугольник значит, 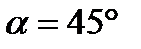
Ответ: 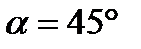
21.Вычислите 
 +
+  c+
c+  c, если,
c, если,  +b+c=0 и |
+b+c=0 и |  |=|
|=|  |=|c|=1.
|=|c|=1.
Решение:
( 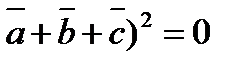 (Возведем обе части в квадрат)
(Возведем обе части в квадрат)
a 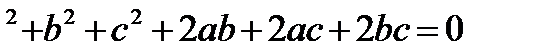
1+1+1+2(ab+ac+bc) =0
2(ab+ac+bc)=-3
ab+ac+bc=-1,5
Ответ:-1,5
22.Вычислите длину вектора  =2i+j-3k.
=2i+j-3k.
Решение:
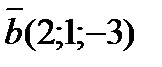
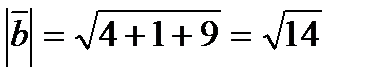
Ответ: 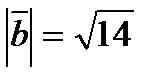
23.Найдите косинус угла между векторами  -
-  и
и  +
+  , если
, если  (1;2;1) и
(1;2;1) и  (2;-1;0).
(2;-1;0).
Решение:
 cos
cos 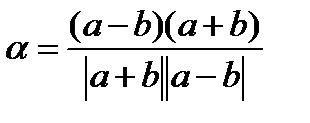
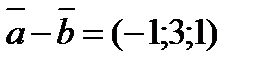
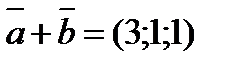
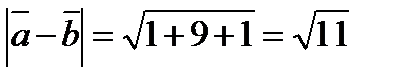
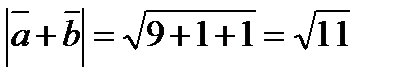
cos 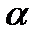 =
= 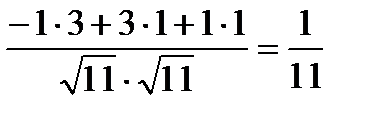
Ответ:cos 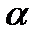
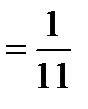
24.Найдите скалярное произведение векторов  и
и  , если |
, если |  |=1, |
|=1, |  |=2, |a+b|=3.
|=2, |a+b|=3.
Решение:
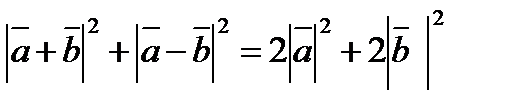
9+ 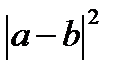 =2+8
=2+8
a-2ab+b 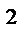 =10-9
=10-9
-2ab+1+4=1
-2ab=-4
ab=2
Ответ:2
25.Найдите угол между векторами р=2  +3
+3  и q=2
и q=2  -3
-3  , если
, если  =i-j+2kи
=i-j+2kи  =2i+2j
=2i+2j
Решение:
cos  =
= 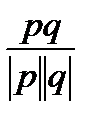 . а(1;-1;2) b(2;2;0)
. а(1;-1;2) b(2;2;0)
p(2*1;2*(-1);2*2+3*2;3*2;3*0)=(8;4;4)
q(2*1;2*(-1);2*2+-3*2;3*2;3*0)=(-4;-8;4)
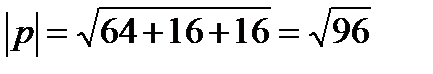
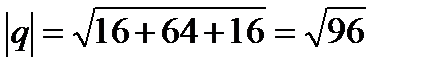
pq=-4*8-8*4+4*4=-32-32+16=-48
cos 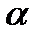 =
= 
Ответ:cos 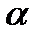 =
= 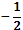
26.В параллелограмме АВСД заданы АВ(-4;-4;-2), СВ(-3;-6;1) и А(3;8;-5). Найдите сумму координат точки пересечения диагоналей.
Решение:
Пусть В( х1;у1;z1) и С(х;у;z)
х 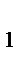 -3=-4 -1-х=-3
-3=-4 -1-х=-3
х1=-1 х=2
у 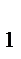 -8=-4 4-у=-6
-8=-4 4-у=-6
у 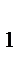 =4 у=10
=4 у=10
z 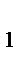 +5=-2 -7-z=1
+5=-2 -7-z=1
z 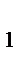 =-7 z=-8
=-7 z=-8
B(-1;4;-7) С(2;10;-8) 
О( 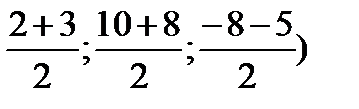 =(
=( 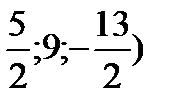
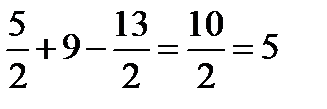
Ответ:5
27.Длина вектора  (х;у;z) равна 5. Найдите ординату вектора
(х;у;z) равна 5. Найдите ординату вектора  , если х=2, z=-
, если х=2, z=- 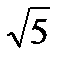
Решение:
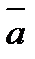 (2;у;-
(2;у;- 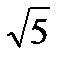 )
)
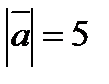
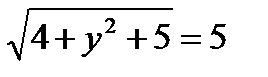
4+у 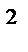 +5=25
+5=25
у 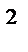 =25-9
=25-9
у 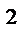 =16
=16
y = 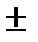 4
4
Ответ: 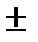 4
4
28.Даны три точки А(1;0;1), В(-1;1;2) и С(0;2;-1). Найдите точку Д(х;у;z), если векторы АВ и СД равны.
Решение:
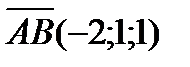
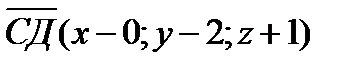
х-0=-2 у-2=1 z+1=1
х=-2, у=3, z=0
Д(-2;3;0)
Ответ:Д(-2;3;0)
В 
29.При каком значении (значениях) k векторы  (6-k;k;2) и
(6-k;k;2) и  (-3;5+5k;-9) перпендикулярны?
(-3;5+5k;-9) перпендикулярны?
Решение:
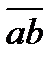 =0
=0
-3(6-k)+k(5+5k)-18=0
-18+3k+5k+5k 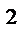 -18=0
-18=0
5k 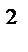 +8k-36=0
+8k-36=0
(+)=-8
(*)=-180
k 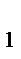 =
= 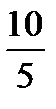 =2 k
=2 k 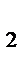 =-
=- 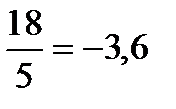
Ответ:k 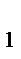 =2, k
=2, k 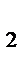 =
= 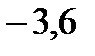
30.При каком значении а векторы АВ и СД коллинеарны, если А(-2;-1;2), В(4;-3;6),
С(-1;а-1;а), Д(-4;-1;а)?
Решение:

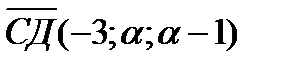
 =
= 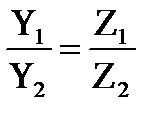 - свойство коллинеарных векторов
- свойство коллинеарных векторов
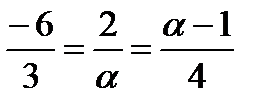
6a=-6
a=-1
Ответ:-1
31.Дано: |  |=4, |
|=4, |  |=1.
|=1. 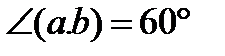 . Найдите cosa, где а – угол между векторами
. Найдите cosa, где а – угол между векторами  -
-  и
и 
Решение:
cos 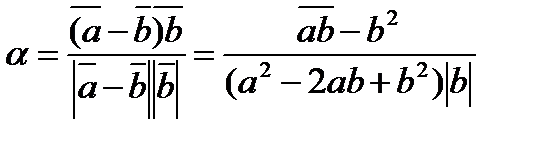
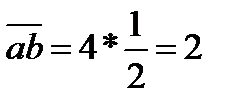
cos 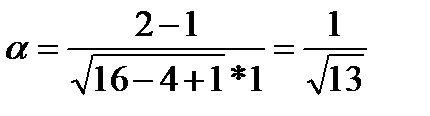
Ответ:cos 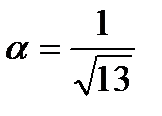
32.Найдите длину вектора a+b+c, если |a|=1 |b|=2, |c|=3,. 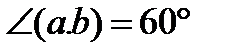 ,
, 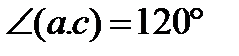 .
.
Решение:
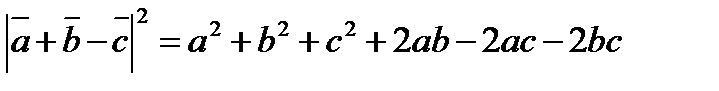
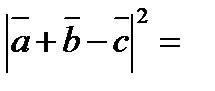 1+4+9+2(2
1+4+9+2(2  0+3
0+3 
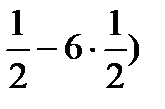
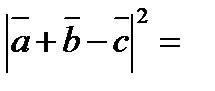 14+2
14+2  (-
(- 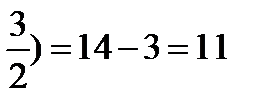
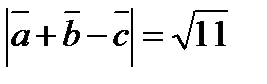
Ответ: 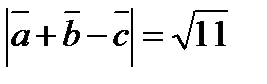
33.В параллелограмме АВСД заданы СД(-3;4;2), СИ(5;-2;4) и А(5;8;0). Найдите расстояние от точки С до начала координат.
Решение:
x 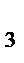 -x
-x 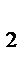 =-3 y
=-3 y 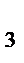 -y
-y 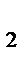 =4 z
=4 z 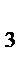 -z
-z 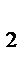 =2
=2
x 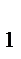 -x
-x 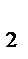 =5 y
=5 y 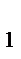 -y
-y 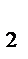 =-2 z
=-2 z 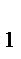 -z
-z 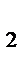 =4
=4
x 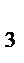 +x
+x 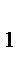 =2+2x
=2+2x 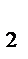 y
y 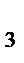 +y
+y 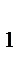 =2+2y
=2+2y 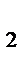 z
z 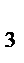 +z
+z 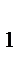 =6+2z
=6+2z
x 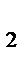 +5=x
+5=x 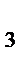 +x
+x 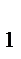 y
y 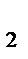 +8=y
+8=y 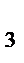 +y
+y 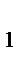 z
z 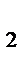 +0=z
+0=z 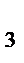 +z
+z 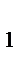
x 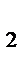 +5=2+2x
+5=2+2x 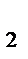 y
y 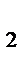 +8=2+2y
+8=2+2y 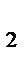 z
z 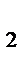 +0=6+2z
+0=6+2z 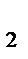
x 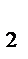 =3 y
=3 y 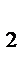 =6 z
=6 z 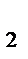 =-6
=-6

Ответ: 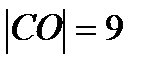
34.Точки А(14;-8;-1), В(7;3;-1), С(-6;4;-1), Д(1;-7;-1) являются вершинами ромба АВСД. Найдите острый угол ромба 
Решение:
cos 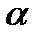 =
= 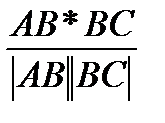
AB(7;11;0) ВС(-13;1;0)
АВ*ВС=91+11=102
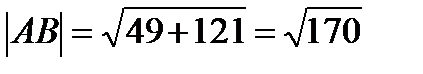
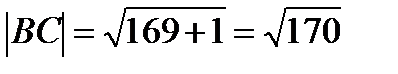

cos 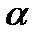 =
= 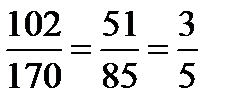
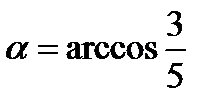
Ответ: 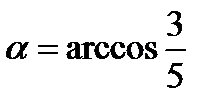
35. Дан треугольник с вершинами в точках А(3;-2;1), В(3;0;2), С(1;2;5). Найдите угол, образованный медианой ВД и основанием АС.
Решение:
точка Д середина отрезка АС  АС (
АС ( 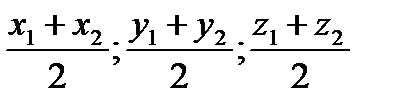 )
)
Д( 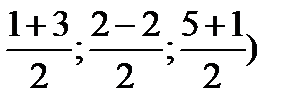 =(2;0;3)
=(2;0;3)
cos  =
= 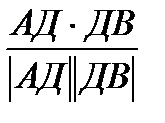
АД(-1;2;2) ВД(-1;0;1)
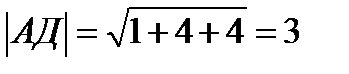
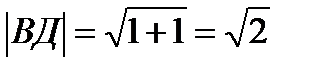
cos 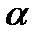 =
= 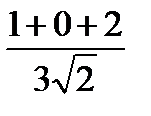 =
= 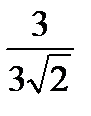 =
= 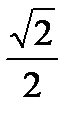
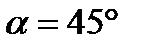
Ответ: 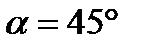
36.В правильном тетраэдре ДАВС с ребром а точка О – центр треугольника АВС. Найдите | 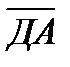 +
+ 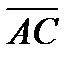 -
- 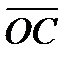 |.
|.
Решение:
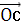 = -
= - 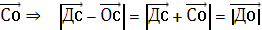
ОВ=R= 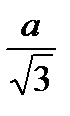
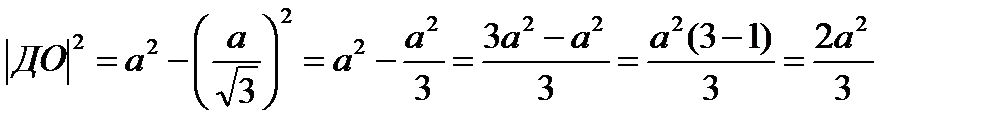
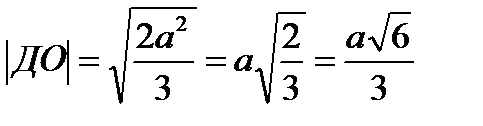
Ответ: 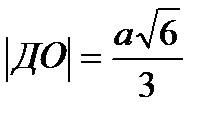
37.Даны три точки: А(1;0;10, В(-1;1;2), С(0;2;-1). Найдите на оси Оz такую точку Д(0;0;с), чтобы векторы 
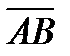 и
и  были перпендикулярны.
были перпендикулярны.
Решение:
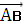
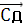 векторы перпендикулярны тогда их скалярное произведение равно нулю.
векторы перпендикулярны тогда их скалярное произведение равно нулю.
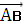 (-2;1;1)
(-2;1;1) 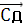 (0;-2;с+1)
(0;-2;с+1)
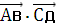 =0-2+с+1=с-1
=0-2+с+1=с-1
с-1=0
с=1
Ответ:1
38.В тетраэдре ДАВС ДА=ДВ=ДС, 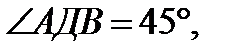
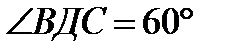 . Вычислите угол между векторами : а)
. Вычислите угол между векторами : а) 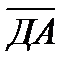 и
и 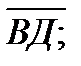 б)
б) 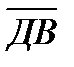 и
и 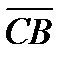 .
.
Решение:
Треугольник СДВ равнобедренный, значит углы при основании равны.
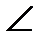 Д=
Д= 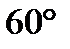
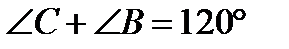
Угол между векторами 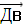 и
и 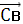 равен
равен 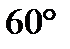
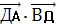 =
= 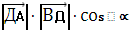 ⇒ cos
⇒ cos 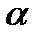 =
= 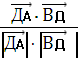
cos 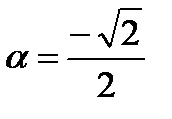
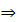 ⇒
⇒ 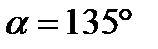
Ответ:600 ; 1350
39. При каком значении а три точки А(2;а; 3), В(3;1;6), С(4;3;9) лежат на одной прямой?
Решение:
А В С
Векторы 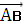 и
и 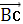 коллинеарные
коллинеарные 

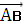 (1;1-а;3)
(1;1-а;3) 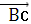 (1;2;3)
(1;2;3)
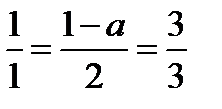
1-а=2
-а=1
а=-1
Ответ:-1
40.Найдите длину интервала значений параметра а, при которых р(-1;2х;х 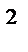 ) и q(5;а;а) при любом х образуют тупой угол.
) и q(5;а;а) при любом х образуют тупой угол.
Решение:
pq<0
-5+2xa+x 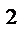 a<0
a<0
x 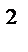 a+2xa-5<0
a+2xa-5<0
D=4а+20а<0
4a(a+5)=0+ - - +
a=0 a=-5 -5 0
0-(-5)=5
Ответ:5
41. Найдите длину вектора  -
- 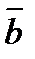 -
- 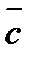 ,если |
,если | 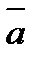 |=2, |
|=2, | 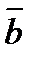 |=3 ,|
|=3 ,| 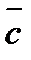 |=4, угол между
|=4, угол между 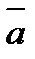 и
и 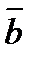 равен
равен 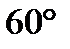 , между
, между 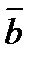 и
и 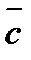 равен
равен 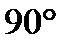 и между
и между 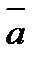 и
и  равен
равен 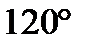 .
.
Решение:
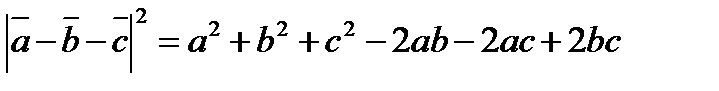 =а
=а 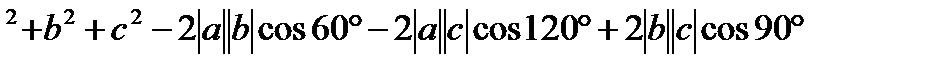
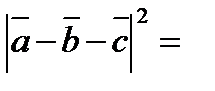 4+9+16-2
4+9+16-2  6
6 
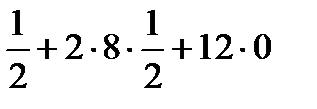
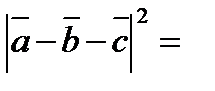 29-6+8=31
29-6+8=31
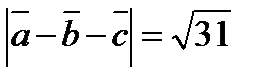
Ответ: 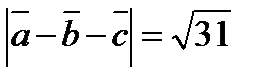
42.Векторы 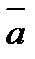 и
и 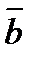 взаимно перпендикулярны, вектор
взаимно перпендикулярны, вектор 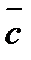 образует с ними угол
образует с ними угол 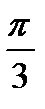 . Зная, что
. Зная, что  =3,
=3,  =5,
=5, 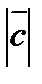 =8, вычислите скалярное произведение
=8, вычислите скалярное произведение 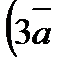 -
- 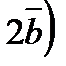
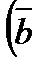 +
+ 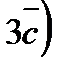 .
.
Решение:
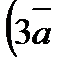 -
- 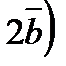
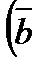 +
+ 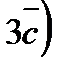 =3ab+9ac-2b
=3ab+9ac-2b  -6bc
-6bc
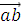 =3
=3  5
5  0=0
0=0
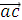 =3
=3  8
8 
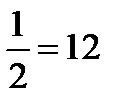
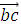 =5
=5  8
8 
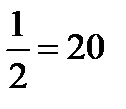
3ab+9ac-2b 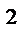 -6bc=3
-6bc=3  0+9
0+9  12-2
12-2  25-6
25-6  20
20
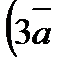 -
- 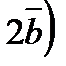
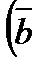 +
+ 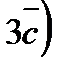 =108-50-120=-62
=108-50-120=-62
Ответ:-62
43.Треугольная пирамида задана координатами своих вершин А(3;0;1), В(-1;4;1), С(5;2;3) и Д(0;-5;4). Вычислите длину вектора 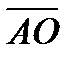 , если О – точка пересечения медиан треугольника ВСД.
, если О – точка пересечения медиан треугольника ВСД.
Решение:
О – центр тяжести ( 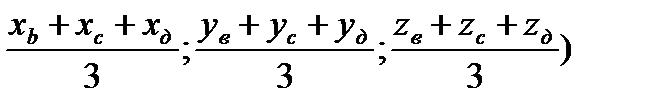
О( 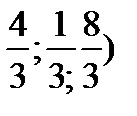
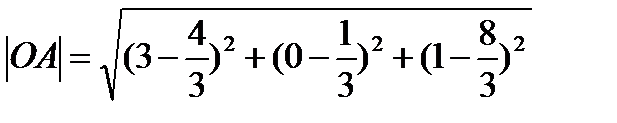 =
= 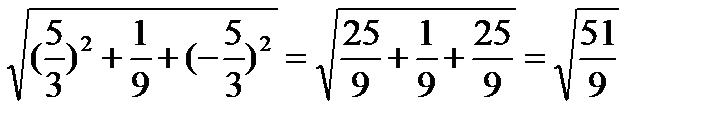
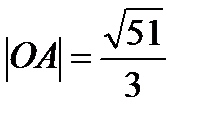
Ответ: 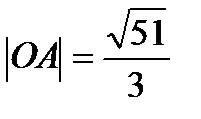
44.  =2,
=2,  =3,
=3,  ,
, 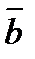 )=120. Найдите cos
)=120. Найдите cos 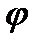 , где
, где 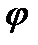 - угол между векторами
- угол между векторами 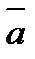 и
и 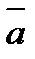 +
+ 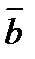 .
.
Решение:
cos 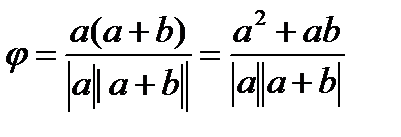
ab=2  3
3  (-
(- 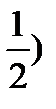 =-3
=-3
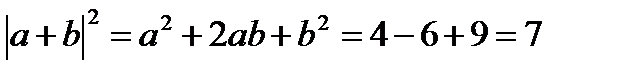
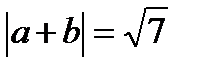
cos 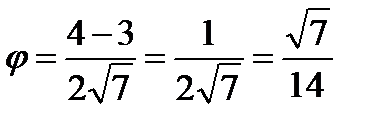
Ответ:cos 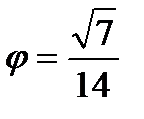
45. Треугольник задан координатами своих вершин А(1;1;2), В(3;4;2) и С(5;6;4). Найдите величину внешнего угла треугольника при вершине В.
Решение:
сos