Тема: Решение прикладных задач

Тема: Решение прикладных задач

Задача № 1

Скорость колеблющегося на пружине груза меняется по закону v=4sinπt (см/с), где t — время в секундах. Какую долю времени из первой секунды скорость движения груза превышала 2 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.

Решение:

Заметим, что в течение первой секунды, то есть при 0⩽t⩽1 выполняется неравенство 0⩽πt⩽π. Из этого неравенства следует, что: sinπt⩾0.

Тогда 4sinπt⩾2,

sinπt⩾

π/6⩽πt⩽5π/6 (см. рис.),

1/6⩽t⩽5/6.

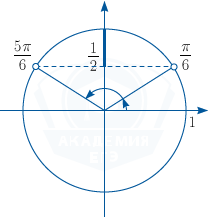
Значит, на первой секунде скорость движения превышала 2 см/с на протяжении 5/6−1/6=2/3≈0,67 секунды.

Ответ:0,67

Задача № 2

Небольшой мячик бросают под острым углом α к плоской горизонтальной поверхности земли. Расстояние, которое пролетает мячик, вычисляется по формуле

L= 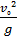sin2α(м), где

V₀=15v0=15 м/с — начальная скорость мячика,

g — ускорение свободного падения (считайте g=10 м/с²).

Определите минимальный угол броска мячика, при котором он сможет перелететь реку шириной 11,25 м. Ответ дайте в градусах.

Решение:

Решим неравенство L⩾11,25.

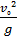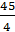
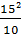sin2α⩾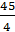

sin2α⩾ .

Так как α — острый угол, то 0<α<2π, 0<2α<π, тогда /π/6⩽2α⩽5π/6, 2α⩾π/6,

α⩾π/12=15∘.

Ответ:15

Домашнее задание: 0.1гл.2§.7 стр.233

1.Скорость колеблющегося на пружине груза меняется по закону

v(t)= 7 sin 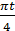(см/с), где t — время в секундах. Какую долю времени из первых двух секунд скорость движения превышала 3,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.

2.Небольшой мячик бросают под острым углом α к плоскости горизонтальной поверхности земли. Расстояние, которое пролетает мячик, вычисляется по формуле L= 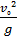sin2α (м), где v₀ = 12 м/с — начальная скорость мячика, а g — ускорение свободного падения (считайте g = 10 м/с²). При каком наименьшем значении угла α (в градусах) мячик перелетит через реку шириной 7,2 м?

12 Следующая ⇒