
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
СЛУЧАЙНЫЕ СОБЫТИЯ. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ.
СЛУЧАЙНЫЕ СОБЫТИЯ. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ.
ЧАСТОТА И ВЕРОЯТНОСТЬ
ПЛАН ЛЕКЦИИ
I. Понятие случайного события. Классическое определение вероятности
II. Элементы комбинаторики
III. Статистическое определение вероятности
IV. Геометрическое определение вероятности
I. Понятие случайного события. Классическое определение вероятности. Теория вероятностей изучает вероятностные закономерности массовых однородных случайных событий.
Все события можно разделить на три вида: достоверные, невозможные, случайные.
Достоверным называется событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий 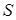 .
.
Невозможным называется событие, которое заведомо не произойдет, если будет осуществлена совокупность условий 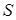 .
.
Случайным называется событие, которое при осуществлении совокупности условий 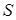 может либо произойти, либо не произойти.
может либо произойти, либо не произойти.
Вероятность – количественная нормированная объективная мера уверенности в том, что некоторое случайное событие произойдет.
Далее вместо слов «осуществлена совокупность условий 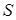 » будем говорить «произведено испытание». Примеры испытаний: бросок монеты или игрального кубика, выстрел по мишени, извлечение шара из урны с разноцветными шарами. Таким образом, событие является результатом или исходом некоторого испытания.
» будем говорить «произведено испытание». Примеры испытаний: бросок монеты или игрального кубика, выстрел по мишени, извлечение шара из урны с разноцветными шарами. Таким образом, событие является результатом или исходом некоторого испытания.
События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании. Примеры несовместных событий: извлечение стандартной и извлечение нестандартной детали из ящика, выпадение герба и выпадение цифры при бросании монеты.
Несколько событий образуют полную группу событий, если в результате испытания наступит хотя бы одно из них. Если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и только одно из этих событий. Примеры полной группы событий: 1) испытание – куплено два лотерейных билета, возможны следующие исходы испытания: первый билет выиграл, второй нет; первый не выиграл, второй выиграл; оба выиграли; оба не выиграли; 2) испытание – выстрел по мишени, возможные исходы испытания: промах и попадание; 3) испытание – бросок игрального кубика, возможные исходы испытания: выпадение одного очка, или двух очков, или трех очков, или четырех очков, или пяти очков, или шести очков.
События называются равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое. Примеры равновозможных событий: 1) испытание – бросок монеты, возможные исходы испытания – выпадение герба или цифры; 2) испытание – бросок игрального кубика, возможные исходы испытания – выпадение одного очка, или двух очков, или трех очков, или четырех очков, или пяти очков, или шести очков.
Элементарным исходом (элементарным событием) называется каждый из возможных результатов испытания.
Те элементарные исходы, в которых интересующее испытателя событие 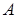 наступает, называются благоприятствующими этому событию или благоприятными.
наступает, называются благоприятствующими этому событию или благоприятными.
Вероятностью события 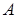 называется отношение числа благоприятствующих этому событию элементарных исходов испытания к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Вероятность события
называется отношение числа благоприятствующих этому событию элементарных исходов испытания к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Вероятность события 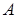 определятся формулой
определятся формулой
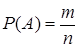 , (1)
, (1)
где 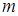 – число исходов, благоприятствующих событию
– число исходов, благоприятствующих событию 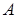 ,
, 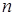 – число всех возможных элементарных исходов испытания. Это определение вероятности называется классическим.
– число всех возможных элементарных исходов испытания. Это определение вероятности называется классическим.
Из определения вероятности следуют ее свойства:
1) вероятность достоверного события равна единице, 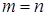 ,
, 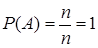 ;
;
2) вероятность невозможного события равна нулю, 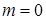 ,
, 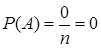 ;
;
3) вероятность случайного события есть положительное число, заключенное между нулем и единицей, 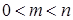 ,
, 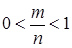 ,
, 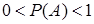 .
.
Таким образом, вероятность любого события удовлетворяет двойному неравенству
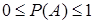 .
.
II. Элементы комбинаторики. На практике часто приходится выбирать из какого-нибудь множества объектов подмножества, обладающие некоторыми свойствами и распределять их по определенному порядку. Например, в группе студентов из 25 человек надо выбрать старосту, его заместителя и профорга или команду из трех человек на спортивные соревнования. Требуется подсчитать, сколькими способами можно сделать такие выборки.
Такие задачи называются комбинаторными, так как в них идет речь о тех или иных комбинациях объектов.
Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов некоторого заданного множества. При этом число элементов множества конечно, а их природа не имеет значения. При непосредственном вычислении вероятностей часто используются формулы комбинаторики. Наиболее употребительными являются три вида комбинаций элементов множеств: перестановки, размещения и сочетания.
Перестановками называются комбинации, состоящие из одних и тех же 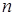 различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок
различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок
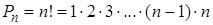 , (2)
, (2)
где 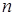 – число элементов рассматриваемого множества,
– число элементов рассматриваемого множества, 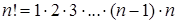 – факториал числа
– факториал числа 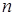 или
или 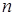 -факториал («эн-факториал») – произведение всех натуральных чисел от единицы до данного натурального числа
-факториал («эн-факториал») – произведение всех натуральных чисел от единицы до данного натурального числа 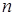 включительно. При решении задач комбинаторики удобно рассматривать
включительно. При решении задач комбинаторики удобно рассматривать 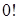 , полагая, по определению,
, полагая, по определению, 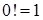 . Отметим свойство факториала, которое следует из его определения и будет использоваться в дальнейшем:
. Отметим свойство факториала, которое следует из его определения и будет использоваться в дальнейшем:
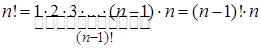 . (3)
. (3)
Пример 1. Сколько трехзначных чисел можно составить из цифр 1, 2, 3 так, чтобы каждая цифра входила в изображение числа только один раз?
Решение. Искомые трехзначные числа состоят из одних и тех же цифр и различаются только порядком их расположения. Поэтому искомое количество трехзначных чисел равно числу перестановок из трех элементов: 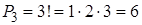 . Эти 6 чисел можно выписать: 123, 132, 213, 231, 312, 321.
. Эти 6 чисел можно выписать: 123, 132, 213, 231, 312, 321.
Ответ: 6.
Пример 2. Сколько пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5 так, чтобы каждая цифра входила в изображение числа только один раз?
Решение: 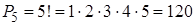 .
.
Пример 3. На четырех карточках написаны буквы А, Б, В, Г. Сколькими способами можно разложить эти буквы друг за другом?
Решение: 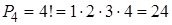 .
.
Сочетаниями называются комбинации, составленные из 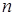 различных элементов по
различных элементов по 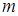 элементов, которые отличаются хотя бы одним элементом. Число всех возможных сочетаний из
элементов, которые отличаются хотя бы одним элементом. Число всех возможных сочетаний из 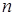 элементов по
элементов по 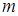 элементов
элементов
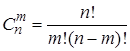 (4)
(4)
или
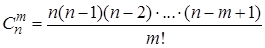 . (4´)
. (4´)
Число сочетаний – это число способов, которыми можно выбрать из 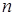 различных элементов группу, состоящую из
различных элементов группу, состоящую из 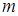 элементов.
элементов.
Пример 4. Сколькими способами можно выбрать три кубика из семи разноцветных кубиков, находящихся в коробке?
Решение. Искомое число способов определяется как число сочетаний из семи кубиков по три с помощью формулы (4):
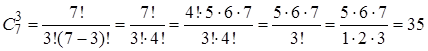 .
.
Ответ: 35.
Число сочетаний обладает свойством симметрии:
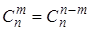 , (5)
, (5)
то есть число способов, которыми можно выбрать 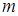 элементов из
элементов из 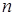 элементов, равно числу способов, которыми можно выбрать
элементов, равно числу способов, которыми можно выбрать 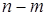 элементов из
элементов из 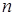 элементов. Другими словами, число способов выбрать
элементов. Другими словами, число способов выбрать 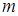 элементов из
элементов из 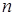 элементов равно числу способов оставить
элементов равно числу способов оставить 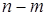 элементов из
элементов из 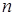 элементов, или число выборок равно числу остатков.
элементов, или число выборок равно числу остатков.
Пример 5. Сколькими способами можно оставить четыре кубика из семи разноцветных кубиков, находящихся в коробке?
Решение. Искомое число способов определяется как число сочетаний из семи кубиков по четыре с помощью формулы (4): 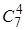 . Пользуясь свойством (5), получим
. Пользуясь свойством (5), получим 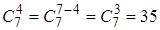 .
.
Размещениями называются комбинации, составленные из 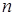 различных элементов по
различных элементов по 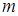 элементов, которые отличаются либо составом элементов, либо их порядком. Число размещений
элементов, которые отличаются либо составом элементов, либо их порядком. Число размещений
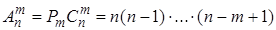 . (6)
. (6)
Если некоторые элементы конечного множества повторяются, то число комбинаций с повторениями определяется по другим формулам:
1) число перестановок с повторениями
 ; (7)
; (7)
2) число сочетаний с повторениями
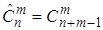 ; (8)
; (8)
3) число размещений с повторениями
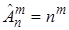 . (9)
. (9)
При решении задач комбинаторики используются следующие правила:
1) правило суммы: если объект 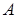 может быть выбран из совокупности объектов
может быть выбран из совокупности объектов 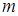 способами, а другой объект
способами, а другой объект 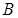 может быть выбран
может быть выбран 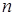 способами, то выбрать либо
способами, то выбрать либо 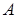 , либо
, либо 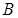 можно
можно 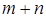 способами;
способами;
2) правило произведения: если объект 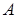 можно выбрать из совокупности объектов
можно выбрать из совокупности объектов 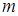 способами и после каждого такого выбора другой объект
способами и после каждого такого выбора другой объект 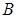 можно выбрать
можно выбрать 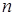 способами, то пару объектов
способами, то пару объектов 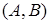 в указанном порядке можно выбрать
в указанном порядке можно выбрать 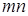 способами.
способами.
III. Статистическое определение вероятности. Наряду с вероятностью одним из основных понятий теории вероятностей является относительная частота.
Относительная частота события – это отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний:
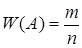 , (10)
, (10)
где 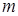 – число появлений события
– число появлений события 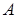 ,
, 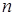 – общее число испытаний.
– общее число испытаний.
Определение вероятности не требует, чтобы испытания проводились в действительности. Определение же относительной частоты предполагает, что испытания были проведены фактически, то есть вероятность вычисляют до опыта, а относительную частоту – после опыта.
Длительные наблюдения показали, что если в одинаковых условиях производятся опыты, в каждом из которых число испытаний велико, то относительная частота обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного значения. Это постоянное значение равно вероятности появления события.
Таким образом, если опытным путем установлена относительная частота, то полученное число можно принять за приближенное значение вероятности.
Слабая сторона классического определения вероятности состоит в том, что часто бывает невозможно представить результат испытания в виде совокупности элементарных событий. Также трудно бывает указать основания, позволяющие считать элементарные события равновозможными. По этой причине наряду с классическим определением вероятности используются другие определения, в частности, статистическое определение: в качестве статистической вероятности события принимается относительная частота этого события или число, близкое к ней.
Свойства вероятности, следующие из ее классического определения, сохраняются и при статистическом определении.
Для существования статистической вероятности события 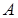 требуется выполнение следующих условий:
требуется выполнение следующих условий:
1) возможность, хотя бы принципиально, производить неограниченное число испытаний, в каждом из которых событие 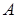 наступает или не наступает;
наступает или не наступает;
2) устойчивость относительных частот появления события 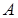 в различных сериях большого числа испытаний.
в различных сериях большого числа испытаний.
Пример 6. Стрелок произвел 20 выстрелов по мишени и 17 раз попал в нее. Найти относительную частоту попаданий в мишень.
Решение. Относительную частоту попаданий в мишень найдем по формуле (10): 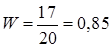 .
.
Недостатком статистического определения является неоднозначность статистической вероятности.
IV. Геометрическое определение вероятности. Для того чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности – вероятности попадания точки в область (отрезок, часть плоскости и т.д.).
Пусть отрезок 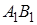 длины
длины 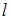 составляет часть отрезка
составляет часть отрезка 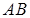 длины
длины 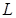 . На отрезок
. На отрезок  наудачу поставлена точка.
наудачу поставлена точка.
Это означает выполнение следующих предположений:
1) поставленная точка может оказаться в любой точке отрезка 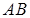 ;
;
2) вероятность попадания точки на отрезок 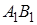 пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка
пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка 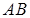 .
.
 |
В этих предположениях вероятность попадания точки на отрезок
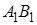 определяется формулой
определяется формулой
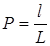 . (11)
. (11)
Пусть плоская фигура 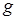 составляет часть плоской фигуры
составляет часть плоской фигуры 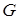 . На фигуру
. На фигуру 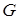 наудачу поставлена точка. Это означает выполнение следующих предположений:
наудачу поставлена точка. Это означает выполнение следующих предположений:
 1) поставленная точка может оказаться в любой точке фигуры
1) поставленная точка может оказаться в любой точке фигуры 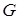 ;
;
2) вероятность попадания точки на фигуру 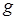 пропорциональна площади этой фигуры и не зависит ни от ее формы, ни от ее расположения относительно фигуры
пропорциональна площади этой фигуры и не зависит ни от ее формы, ни от ее расположения относительно фигуры 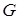 .
.
В этих предположениях вероятность попадания точки в фигуру 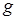 определяется формулой
определяется формулой
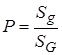 , (12)
, (12)
где 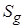 – площадь фигуры
– площадь фигуры 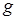 ,
, 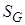 – площадь фигуры
– площадь фигуры 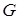 .
.
Данные выше определения являются частными случаями общего определения геометрической вероятности. Если обозначить меру (длину, площадь, объем) области 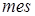 , то вероятность попадания точки, брошенной наудачу (в указанном выше смысле) в область
, то вероятность попадания точки, брошенной наудачу (в указанном выше смысле) в область 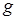 – часть области
– часть области 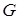 , определяется формулой
, определяется формулой
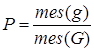 . (13)
. (13)
При классическом определении вероятность достоверного события равна единице, а невозможного – нулю. Справедливы и обратные утверждения: если вероятность события равна единице, то событие достоверно; если нулю – то невозможно. В случае геометрического определения вероятности обратные утверждения не имеют места. Например, вероятность попадания брошенной точки в одну определенную точку области 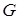 равна нулю, но это событие может произойти и, следовательно, не является невозможным.
равна нулю, но это событие может произойти и, следовательно, не является невозможным.
Пример 7. На плоскости начерчены две концентрические окружности радиусами 1 и 2 см соответственно. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадет в кольцо, образованное двумя окружностями. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади этой фигуры и не зависит от ее расположения относительно большого круга.
Решение. Площадь кольца 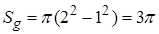 . Площадь большого круга
. Площадь большого круга 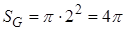 . Искомую вероятность найдем по формуле (12):
. Искомую вероятность найдем по формуле (12): 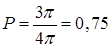 .
.
Пример 8. Задача о встрече. Два студента договорились встретиться в определенном месте между 17 и 18 часами дня. По договоренности, студент, пришедший первым, ждет второго в течение 15 минут, а потом уходит. Найти вероятность того, что встреча состоится, если каждый студент наудачу выбирает время своего прихода между 17 и 18 часами.
 |
Решение. Будем вести отсчет времени в минутах от 17:00. Обозначим моменты прихода на встречу первого и второго студента соответственно через
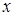 и
и  . По условию задачи величины
. По условию задачи величины 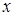 и
и 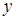 могут принять любые значения от 0 до 60 минут, то есть должны выполняться двойные неравенства:
могут принять любые значения от 0 до 60 минут, то есть должны выполняться двойные неравенства: 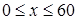 ,
,  . Введем прямоугольную систему координат
. Введем прямоугольную систему координат 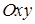 . В этой системе координат указанным двойным неравенствам удовлетворяют координаты всех точек, принадлежащих квадрату OABC (рисунок). Поэтому квадрат OABC является фигурой
. В этой системе координат указанным двойным неравенствам удовлетворяют координаты всех точек, принадлежащих квадрату OABC (рисунок). Поэтому квадрат OABC является фигурой 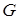 , координаты точек которой представляют собой все возможные значения моментов прихода студентов на встречу.
, координаты точек которой представляют собой все возможные значения моментов прихода студентов на встречу.
Встреча состоится, если разность между моментами прихода студентов по абсолютной величине не превысит 15 минут, то есть если 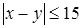 . Это неравенство эквивалентно двойному неравенству
. Это неравенство эквивалентно двойному неравенству 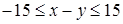 или системе неравенств
или системе неравенств
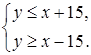 (14)
(14)
Точки квадрата OABC, координаты которых удовлетворяют первому неравенству системы, лежат ниже прямой 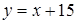 , а точки, координаты которых удовлетворяют второму неравенству системы, лежат выше прямой
, а точки, координаты которых удовлетворяют второму неравенству системы, лежат выше прямой 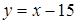 . Из рисунка видно, что множество точек, удовлетворяющих системе неравенств (14), образует шестиугольник ODEBFK. Этот шестиугольник является фигурой
. Из рисунка видно, что множество точек, удовлетворяющих системе неравенств (14), образует шестиугольник ODEBFK. Этот шестиугольник является фигурой  , координаты точек которой определяют моменты прихода студентов
, координаты точек которой определяют моменты прихода студентов 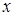 и
и 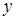 , благоприятные для их встречи.
, благоприятные для их встречи.
Таким образом, вероятность встречи студентов
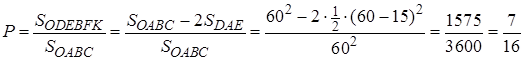 .
.
Ответ: 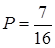 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|