
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Разработка программы решения системы двух уравнений с двумя неизвестными по теме Матричные игры.
10."Разработка программы решения системы двух уравнений с двумя неизвестными по теме Матричные игры. "
11. Задание:
В течение пяти дней (рабочая неделя) рабочий изготавливает детали семи различных типов. Известно количество изготовленных им деталей за каждый день и стоимость изготовления одной детали каждого типа (стоимость изготовления детали не меняется). Написать программу, которая вводит данные, выполняет расчет и выводит на экран:• исходные данные в виде таблицы, где перечислены наименования деталей, стоимость изготовления, количество деталей, изготовленных за каждый день;• количество деталей каждого типа, изготовленных за неделю;• заработок за каждый день;• день с наибольшим заработком.
12. Задание:
Спортивный магазин продавал в течение года 7 моделей роликовых коньков по цене, устанавливаемой в начале каждого месяца. Написать программу на языке VBA, которая вводит исходные данные, выполняет расчеты и выводит на экран: • исходные данные в виде таблицы, где перечислены модели роликовых коньков, цены на них в каждом месяце, количество проданных роликовых коньков одной модели в течение каждого месяца; • доход от продажи каждой модели коньков за год; • доход от продажи всех моделей коньков за каждый месяц; • общий доход от продажи всех моделей коньков за год; • наименование модели коньков, принесшей наименьший доход за первые 6 месяцев.
13. Задание:
Разработать проект «Поиск фигуры» содержащий форму на который требуется найти фигуру путем перемещения указателя мыши. Этапы поиска фигуры должны отображаться соответствующими сообщениями в строке состояния. Фигура не будет видна на форме до тех пор, пока указатель мыши не попадет на нее.
14. Задание:
Разработать проект «Просмотр картинок», содержащий форму, на которой можно просматривать картинки, находящиеся на жестком диске, сетевом и на DVD-ROM.
15. Задание:
Программа выбирает слово и рисует на экране столько прочерков, сколько букв в этом слове. Отгадать, какое слово загадано программой. В каждый ход играющий указывает одну букву.
Если названа буква, входящая в состав слова, она подставляется вместо соответствующего прочерка. В противном случае играющий теряет 1 очко. В начальный момент у играющего 15 очков.
Сколько очков у играющего будет на момент окончания игры.
16. Задание:
Два числа называют дружественными, если каждое из них равно сумме делителей другого, кроме самого этого числа, например, 220 и 284:
1+2+4+5+10+11+20+22+44+55+110 = 284
1+2+4+71+142 = 220
Заданы два натуральных числа n и m. Найти все дружественные числа в диапазоне от n до m.
В основе метода решения задачи лежит поиск суммы всех делителей чисел, принадлежащих указанному интервалу, и затем поиск пар дружественных чисел по определенным суммам делителей.
При решении задачи введено ограничение: максимальное рассматриваемое число не должно превышать 15000.
17. Задание:
Записать программу решения задачи вычисления приближенного значения интеграла для функции f(x) в интервале(a;b) с числом, точек разбиения n по формуле правых прямоугольников.
Для контроля правильности полученного решения включить в программу операторы вычисления интеграла по формуле Ньютона–Лейбница, используя приведенную в таблице первообразную функцию F(x), предварительно проверив равенство  .
.
Если погрешность превышает 0.0001, подберите такое число разбиений n, при котором погрешность будет не выше этого числа.
Решите эту же задачу средствами табличного процессора Microsoft Excel.
f(x) =  .
.
a = 0.1;
b = 0.7;
n = 104;
F(x) = 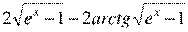 .
.
18. Задание:
Написать программу решить системы линейных уравнений двумя способами:
по формулам Крамера;
методом обратной матрицы.
Продублировать решение средствами табличного процессора Microsoft Excel.
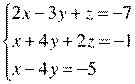
19. Задание:
Написать программу для решения системы линейных уравнений методом Гаусса
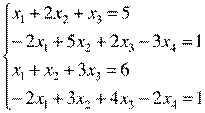
20. Задание:
Записать программу решения задачи вычисления приближенного значения интеграла для функции f(x) в интервале(a;b) с числом, точек разбиения n по формуле правых прямоугольников.
Для контроля правильности полученного решения включить в программу операторы вычисления интеграла по формуле Ньютона–Лейбница, используя приведенную в таблице первообразную функцию F(x), предварительно проверив равенство  .
.
Если погрешность превышает 0.0001, подберите такое число разбиений n, при котором погрешность будет не выше этого числа.
Решите эту же задачу средствами табличного процессора Microsoft Excel.
f(x) = 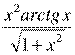 .
.
a = 0.02;
b = 0.9;
n = 22;
F(x) = 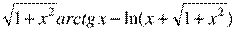 .
.
21. Задание:
Написать программу для решения системы линейных уравнений методом Гаусса
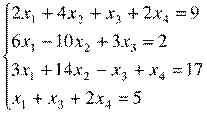
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|