Контакты

Случайная статья

Показательные неравенства. Повторение

Стр 1 из 3Следующая ⇒

Показательные неравенства. Повторение

Показательными неравенствами называют неравенства вида:

, , ,

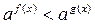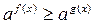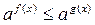
где 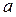— положительное число, отличное от 1, и неравенства, сводящиеся к этому виду.

Решение простейших показательных неравенств основано на свойствах показательной функции, поэтому повторим их.

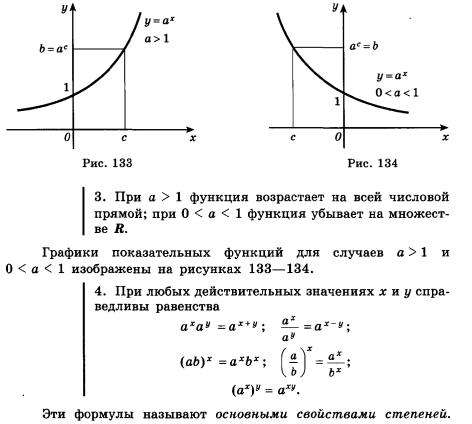
Если 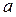>1, то показательные неравенства

, , ,

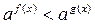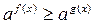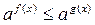
равносильны соответственно неравенствам того же смысла

, , , .

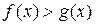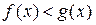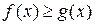Если 0< 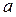<1, то показательные неравенства

, , ,

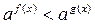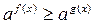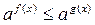
равносильны соответственно неравенствам противоположного смысла

, , , .

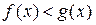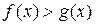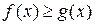Пример 1. Решить неравенство: .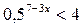

Решение:

Пользуясь тем, что 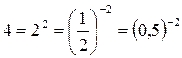, сводим наше неравенство к простейшему:

Показательная функция 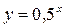- убывает, так как .

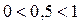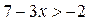
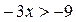
Ответ:

Пример 2. Решить неравенство: .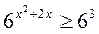

Показательная функция 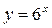- возрастает, так как .

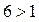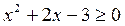
Решим данное неравенство методом интервалов, для этого найдём нули функции .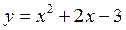

;

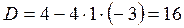
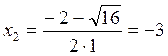
Отметим нули функции на числовой прямой:

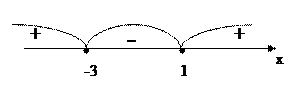
Ответ: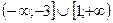

Контрольные вопросы

1. Какие неравенства называют показательными?

2. На чем основано решение простейших показательных неравенств?

3. Какую функцию называют показательной?

4. Перечислите основные свойства показательной функции (с рисунками).

5. К каким неравенствам сводится решение неравенств , , 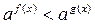, , 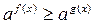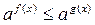если 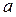>1?

6. К каким неравенствам сводится решение неравенств , , 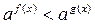, , 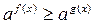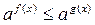если 0< 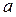<1?

7. Приведите два примера решения показательных неравенств.

12 3 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.