
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Несобственные интегралы
Несобственные интегралы
1. 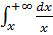
Подынтегральная функция 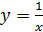 непрерывна на полуинтервале
непрерывна на полуинтервале 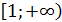 . Простейший табличный интеграл. Применение формулы Ньютона-Лейбница, как в определенном интеграле, но под знаком предела. Несобственный интеграл расходится.
. Простейший табличный интеграл. Применение формулы Ньютона-Лейбница, как в определенном интеграле, но под знаком предела. Несобственный интеграл расходится.
2. 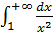
Подынтегральная функция 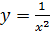 непрерывна на полуинтервале
непрерывна на полуинтервале 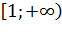 . Решаем с помощью формулы. Простейший интеграл от степенной функции. Минус вынести за знак предела. Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.
. Решаем с помощью формулы. Простейший интеграл от степенной функции. Минус вынести за знак предела. Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.
3. 
Подынтегральная функция непрерывна на 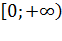 . Найти первообразную функцию F(x). В знаменателе получаем квадрат. Делается это путем замены.
. Найти первообразную функцию F(x). В знаменателе получаем квадрат. Делается это путем замены. 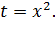 Формула. Константу лучше вынести за знак предела. Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница.
Формула. Константу лучше вынести за знак предела. Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница.
4. 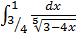
Подынтегральная функция имеет бесконечный разрыв в точке 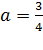 . Вычислим неопределенный интеграл. Замена: t = 3 – 4x. Вычислим несобственный интеграл. Подставляем верхний и нижний предел по формуле Ньютона Лейбница.
. Вычислим неопределенный интеграл. Замена: t = 3 – 4x. Вычислим несобственный интеграл. Подставляем верхний и нижний предел по формуле Ньютона Лейбница.
5. 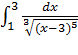
Подынтегральная функция имеет бесконечный разрыв в точке b = 3. Предел левосторонний, к точке b = 3 мы приближаемся по оси OX слева. Подставляем под корень предельное значение b = 3 – 0. Несобственный
6. Несобственный интеграл с точкой разрыва на отрезке интегрирования
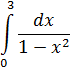
Подынтегральная функция терпит бесконечный разрыв на отрезке в точке 1. Представим несобственный интеграл в виде суммы двух несобственных интегралов.
7. 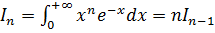
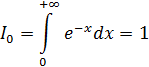
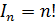
8. 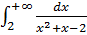
Разложим на множители знаменатель. Разложим дробь на сумму дробей. Подстановка u=x−1. Табличный интеграл. Обратная замена. Подстановка u=x+2. Табличный интеграл. Обратная замена. Формула Ньютона-Лейбница
9. 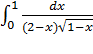
Замена u=√1-x. табличный интеграл, обратная замена. Предел при b -> 1
10. 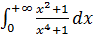
Разложим на множители знаменатель. Разложим на сумму дробей. Разложим на сумму интегралов. 1) Выделим полный квадрат, Подстановка u=√2x+1. Табличный интеграл. Обратная замена. 2) Выделим полный квадрат, Подстановка u=√2x-1. Табличный интеграл. Обратная замена. Предел при b -> +∞.
11. 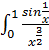
Подынтегральная функция не показывает сходимости интеграла. Сделаем в интеграле замену переменной. Полученный интеграл сходится условно.
12. 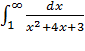
Для вычисления неопределенного интеграла используется интегрирование путем подведения под знак дифференциала. Несобственный интеграл сходится.
13. 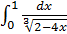
Для вычисления неопределенного интеграла используется интегрирование путем подведения под знак дифференциала. Несобственный интеграл сходится.
14. 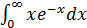
Для вычисления неопределенного интеграла применяется метод интегрирования по частям. Несобственный интеграл сходится.
15. 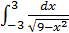
В данном случае подынтегральная функция имеет две особые точки x1=-3 и x2=3. Пользуясь определением несобственного интеграла и учитывая непрерывность первообразной, получаем 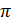 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|