Несобственный интеграл

Несобственный интеграл

Основные определения

О1. Понятие определенного интеграла существенно использовало два требования:

1) конечность промежутка [a, b], по которому идет интегрирование;

2) ограниченность интегрируемой функции f(x).

Если эти требования не выполняются, то необходим дополнительный переход к пределу, и возникающий при этом переходе интеграл принято называть несобственным.

О2. Несобственный интеграл 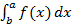называется сходящимся, если существует конечный предел слева функции F(β) в точке b. Тогда, 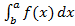= = 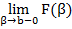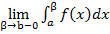. В противном случае несобственный интеграл 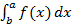называется расходящимся.

Несобственный интеграл первого рода

Несобственный интеграл первого рода возникает, когда по крайней мере одно из чисел в 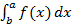a или b бесконечно.

Рассмотрим 3 случая:

Для начала надо убедиться, что наш несобственный интеграл непрерывен на всём интервале и не терпит нигде разрыва.

1) Рассмотрим сначала ситуацию, когда нижний предел интегрирования конечен, а верхний равен +∞: т.е. .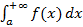

Для вычисления такого несобственного интеграла необходимо:

· вычислить первообразную и перейти к пределу;

· воспользоваться формулой Ньютона-Лейбница.

Пример 1:

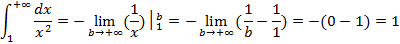
Пример 2:

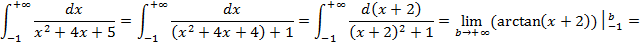
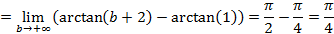
Пример 3:

Несобственный интеграл расходится.

Пример 4:

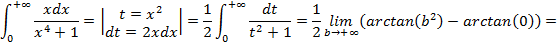
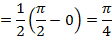
Пример 5:

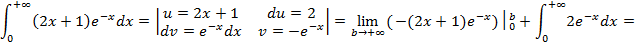
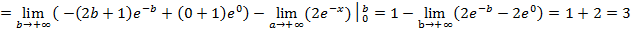
2) Рассмотрим теперь вариант, когда нижний предел интегрирования равен −∞, а верхний конечен, т.е. .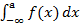

По алгоритму этот вариант ничем не отличается от предыдущего. Только теперь мы должны a устремить к −∞ (a→−∞).

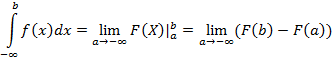
Пример 6:

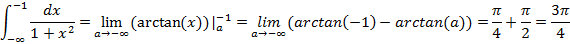
Пример 7:

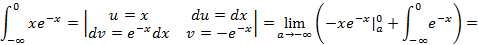
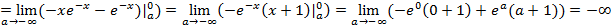
Несобственный интеграл расходится.

Пример 8:

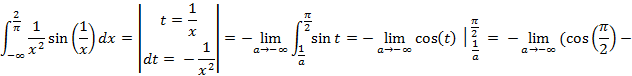
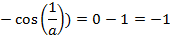
3) И последний вариант, когда нижний предел равен −∞, а верхний – +∞, т.е. .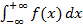

Для решения интегралов такого типа нужно предварительно представить выражение в виде суммы двух несобственных интегралов, один из которых с конечным верхним пределом интегрирования, другой – с конечным нижним пределом интегрирования, т.е.

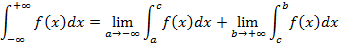
Причём этот несобственный интеграл считается сходящимся, если оба предела существуют, когда a и b независимо друг от друга неограниченно возрастают по абсолютной величине.

Пример 9:

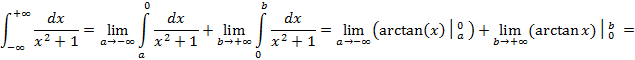
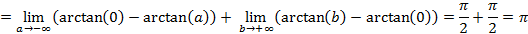
Пример 10:

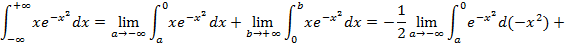
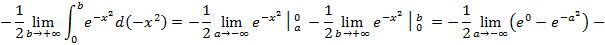
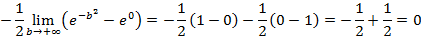
Пример 11:

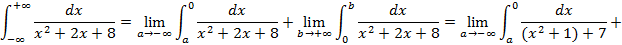
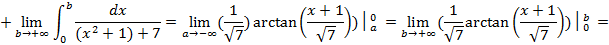
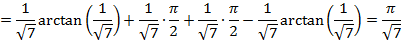
Несобственный интеграл второго рода

Если функция f(x) терпит бесконечный разрыв (не существует):

· в точке x = a;

· в точке x = b;

· в обеих точках сразу;

· на отрезке интегрирования,

то говорят о несобственном интеграле второго рода.

Прежде чем начать решение, мы должны проверить пределы интегрирования, подставив в подынтегральную функцию. Затем перейти к пределу, вычислить первообразную и воспользоваться модифицированной формулой Ньютона-Лейбница.

1) Если подынтегральная функция не существует в точке x = a, то предел стремится уже не к бесконечности, а к значению «a» справа.

Пример 12:

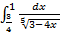– подынтегральная функция терпит бесконечный разрыв в точке a= . Найдём неопределённый интеграл.

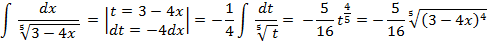
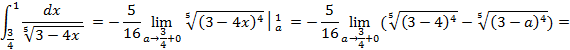
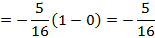
2) Если подынтегральная функция не существует в точке x = b, то предел стремится к значению «b» слева.

Пример 13:

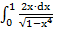– подынтегральная функция терпит бесконечный разрыв в точке b= 1.

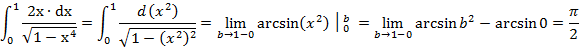
3) Если подынтегральная функция не существует на обоих концах отрезка, то представляем выражение в виде суммы двух несобственных интегралов и используем методику из прошлых случаев.

Пример 14:

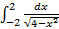– подынтегральная функция терпит бесконечные разрывы в обоих концах отрезка.

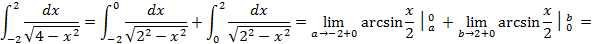
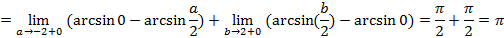
4) Если подынтегральная функция терпит разрыв на отрезке интегрирования, то представляем выражение в виде суммы, разбивая её в точке разрыва.

Пример 15:

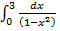– подынтегральная функция терпит бесконечный разрыв в точке x = 1.

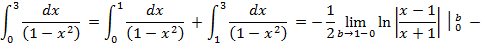
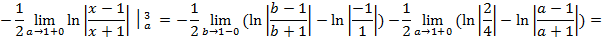
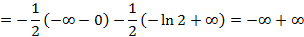
Не существует в общем случае.