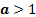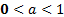Логарифмические неравенства.. Теоретический материал для самостоятельного изучения. Пример 1.. Пример 2. . Решить самостоятельно

Логарифмические неравенства.

Ссылка на видео урок https://resh.edu.ru/subject/lesson/3852/main/199123/

Теоретический материал для самостоятельного изучения

Логарифмические неравенства – это неравенства вида 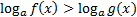, где 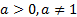и неравенства, сводящиеся к этому виду.

Способы решения логарифмических неравенств основаны на монотонности логарифмической функции в зависимости от основания логарифма. Функция возрастает, если 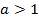и убывает, если .

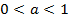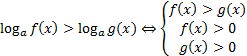
(знак неравенства сохраняется)

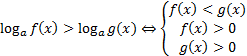
(знак неравенства меняется)

Пример 1.

Решить неравенство .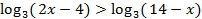

Решение:

Основание логарифма 3 > 1, значит используем 1 схему.

; ; .

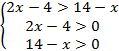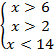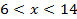Ответ: (6; 14)

Пример 2.

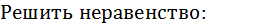log_0,5(2x - 3) < log_0,5(6– x)

Решение. Основание логарифма равно 0,5, значит логарифмическая функция y = log_0,5t убывающей. Значит, при переходе от логарифмического неравенства к алгебраическому знак неравенства меняется на противоположный. Учитываем ОДЗ : выражения, записанные под знаком логарифма, должны быть положительными. Переходим к системе неравенств:

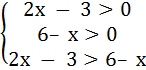
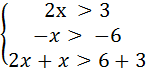
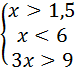
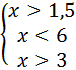
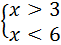
Ответ: (3; 6).

Решить самостоятельно

log₅(x + 12) < log₅(8 – 3x)

log₄(5x - 20) < log₄(4 + x)