
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Логарифмическая производная. Дифференцирование показательно степенной функции.
Логарифмическая производная. Дифференцирование показательно степенной функции.

При дифференцировании показательно степенной функции 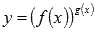 или громоздких дробных выражений удобно пользоваться логарифмической производной. В этой статье мы рассмотрим примеры ее применения с подробными решениями.
или громоздких дробных выражений удобно пользоваться логарифмической производной. В этой статье мы рассмотрим примеры ее применения с подробными решениями.
Дальнейшее изложение подразумевает умение пользоваться таблицей производных, правилами дифференцирования и знание формулы производной сложной функции.
Вывод формулы логарифмической производной.
Сначала производим логарифмирование по основанию e, упрощаем вид функции, используя свойства логарифма, и далее находим производную неявно заданной функции:
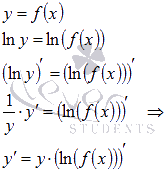
Для примера найдем производную показательно степенной функции x в степени x.
Логарифмирование дает 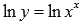 . По свойствам логарифма
. По свойствам логарифма 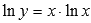 . Дифференцирование обеих частей равенства приводит к результату:
. Дифференцирование обеих частей равенства приводит к результату:
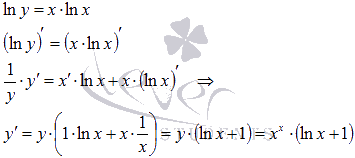
Ответ: 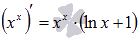 .
.
Этот же пример можно решить и без использования логарифмической производной. Можно провести некоторые преобразования и перейти от дифференцирования показательно степенной функции к нахождению производной сложной функции:
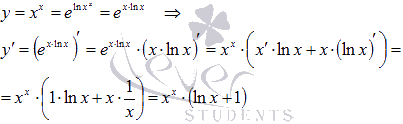
Пример.
Найти производную функции 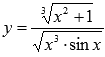 .
.
Решение.
В этом примере функция 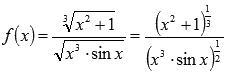 представляет собой дробь и ее производную можно искать с использованием правил дифференцирования. Но в силу громоздкости выражения это потребует множества преобразований. В таких случаях разумнее использовать формулу логарифмической производной
представляет собой дробь и ее производную можно искать с использованием правил дифференцирования. Но в силу громоздкости выражения это потребует множества преобразований. В таких случаях разумнее использовать формулу логарифмической производной  . Почему? Вы сейчас поймете.
. Почему? Вы сейчас поймете.
Найдем сначала 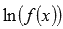 . В преобразованиях будем использовать свойства логарифма (логарифм дроби равен разности логарифмов, а логарифм произведения равен сумме логарифмов, и еще степень у выражения под знаком логарифма можно вынести как коэффициент перед логарифмом):
. В преобразованиях будем использовать свойства логарифма (логарифм дроби равен разности логарифмов, а логарифм произведения равен сумме логарифмов, и еще степень у выражения под знаком логарифма можно вынести как коэффициент перед логарифмом):

Эти преобразования привели нас к достаточно простому выражению, производная которого легко находится:
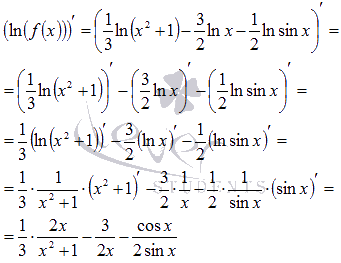
Подставляем полученный результат в формулу логарифмической производной и получаем ответ:
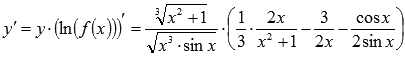
Для закрепления материала приведем еще пару примеров без подробных объяснений.
Пример.
Найдите производную показательно степенной функции 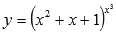
Решение.
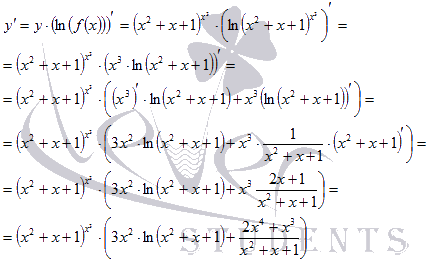
Пример.
Найдите производную функции 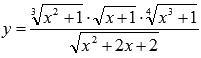 .
.
Решение.
Воспользуемся формулой логарифмической производной:
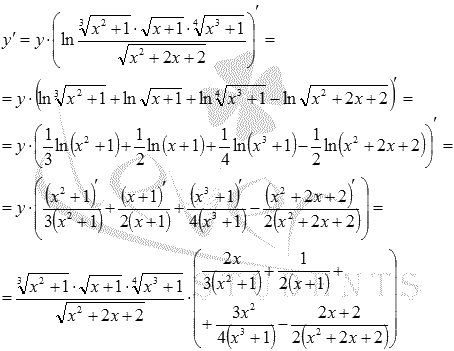
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|