
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Криволинейные интегралы I–го и II–го рода.
Криволинейные интегралы I–го и II–го рода.
1. Криволинейные интегралы I рода.
а. Если плоская кривая L задана непрерывно дифференцируемой функцией y=y(x), 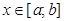 , то криволинейные интегралы I рода вычисляется:
, то криволинейные интегралы I рода вычисляется:
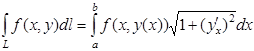
б. Если плоская кривая L задана параметрическими уравнениями x=x(t) y=y(t), где x(t) и y(t) непрерывно дифференцируемые функции параметра t при, токриволинейные интегралы I рода вычисляется:
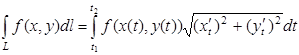
в. Если плоская кривая L задана полярным уравнением r=r(j), 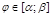 , то криволинейные интегралы I рода вычисляется:
, то криволинейные интегралы I рода вычисляется:
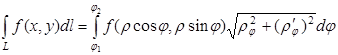
Задача. Вычислить криволинейный интеграл 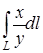 , где L дуга параболы
, где L дуга параболы 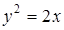 заключенная между точками (2,2) и (8,4).
заключенная между точками (2,2) и (8,4).
1. 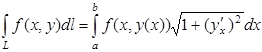
2. 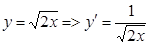 ,
, 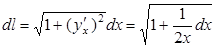 , при
, при 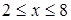
3. 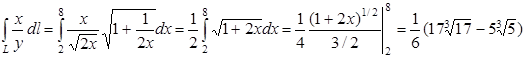
 Задача. Вычислить криволинейный интеграл
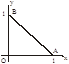
Задача. Вычислить криволинейный интеграл 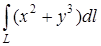 , где L контур треугольника АВО с вершинами А(1,0) В(0,1) О(0,0).
, где L контур треугольника АВО с вершинами А(1,0) В(0,1) О(0,0).
1. 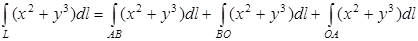
а. 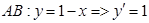 ,
, 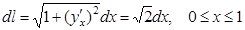
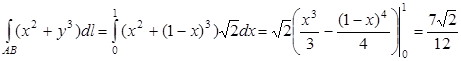
б. 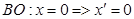 ,
, 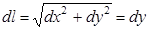
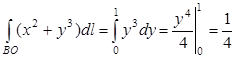
в. 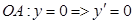 ,
, 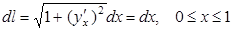
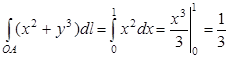
2. 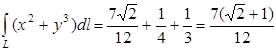
Задача. Вычислить 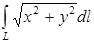 , где L: контур окружности
, где L: контур окружности 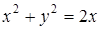
1. Перейдем к полярной системе координат
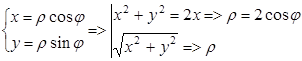
2. 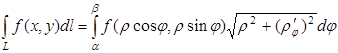
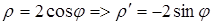 ,
,
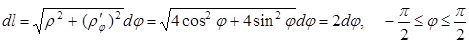
3. 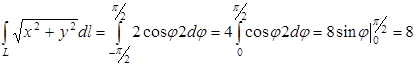
Задача. Вычислить криволинейный интеграл I рода 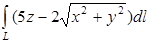 по пространственной кривой, где L– дуга кривой заданной параметрический x=t cost, y=t sint z=t, при 0≤t≤π.
по пространственной кривой, где L– дуга кривой заданной параметрический x=t cost, y=t sint z=t, при 0≤t≤π.
1. а. 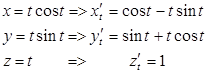
б. 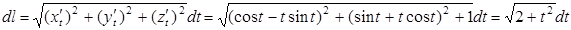
в. 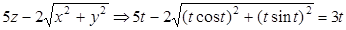
2. 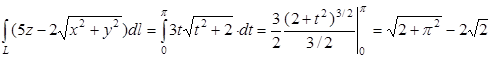
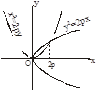 Задача. Вычислить криволинейный интеграл
Задача. Вычислить криволинейный интеграл 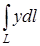 , где L – дуга параболы
, где L – дуга параболы 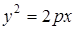 , отсеченная параболой
, отсеченная параболой 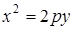
1. 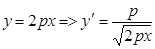 ,
,
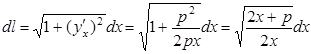
2. 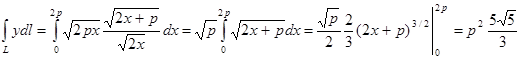
2. Криволинейные интегралы II рода (по координатам)
а. Если плоская кривая задана уравнением y=y (x) и при перемещении из точки А в точку В х меняется от а до b, то криволинейные интегралы II рода вычисляется:
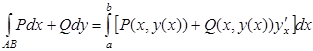
б. Если плоская кривая задана параметрическими уравнениями x=x(t), y=y(t) и при перемещении из точки А в точку B и параметр t меняется от α до β, то криволинейные интегралы II рода вычисляется:
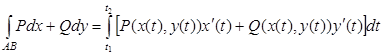
Задача. Вычислить 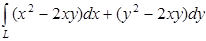 где, L – дуга параболы
где, L – дуга параболы 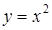 пробегаемой от точки А(–1,1) до точки В(1,1).
пробегаемой от точки А(–1,1) до точки В(1,1).
1. 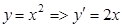 , при
, при 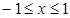
2. 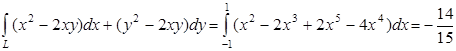
Задача. Вычислить 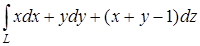 , где L – отрезок прямой, соединяющий точки А(1,1,1) и В(2,3,4).
, где L – отрезок прямой, соединяющий точки А(1,1,1) и В(2,3,4).
1. Т.к. мы имеем пространственную линию, то данный интеграл можно вычислить перейдя к параметрическим уравнениям прямой проходящей через точку A и параллельно вектору 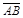
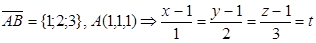
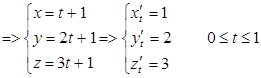
2. 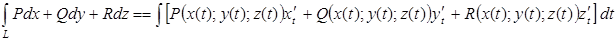
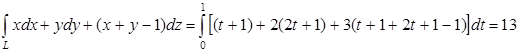
Задача. Вычислить 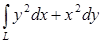 интеграл, где L:
интеграл, где L: 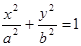 верхняя половина эллипса пробегаемая по ходу часовой стрелки.
верхняя половина эллипса пробегаемая по ходу часовой стрелки.
1. Воспользуемся параметрическими уравнениям эллипса:
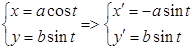 , при
, при 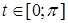 пробегая от
пробегая от 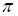 до 0.
до 0.
2. 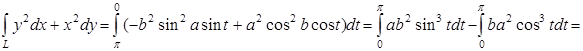
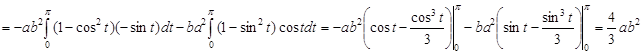
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|